Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.9 - Ex. 46
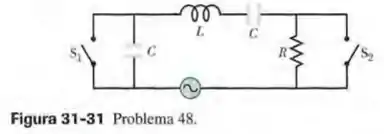
A Fig. 31-31 mostra um circuito , alimentado por um gerador, que possui dois capacitores iguais e duas chaves. A amplitude da força eletromotriz é e a frequência do gerador é . Com as duas chaves abertas, a corrente está adiantada em relação à tensão. Com a chave fechada e a chave aberta, a corrente está adiantada em relação à tensão. Com as duas chaves fechadas, a amplitude da corrente é . Determine o valor (a) de ; (b) de ; (c) de .
Passo 1
A questão fornece um circuito com duas chaves que podem ser abertas ou fechadas. Devemos encontrar a resistência, a capacitância e a indutância do circuito. Vamos analisar primeiro o que acontece com as duas chaves fechadas.
Se fecharmos as duas chaves, o resistor e o segundo capacitor estarão em curto e podem ser descartados. Assim, a impedância do circuito será dada por
Por outro lado,
Portanto
Detalhe: aqui, apenas um capacitor está no circuito, de modo que
Passo 2
Agora vamos fechar a chave 1 e manter a chave 2 aberta. Nesse caso, . Sabemos que
Portanto,
Logo,
Passo 3
Agora vamos deixar as duas chaves abertas. Neste caso, . Note que agora, os dois capacitores estão no circuito e eles estão em série, de modo que a capacitância equivalente será
Portanto, neste caso
Assim, como temos a fase:
Como e , segue que
Assim,
Passo 4
Temos que resolver o sistema:
Resolvendo o sistema, obtemos
A frequência angular será dada por
Passo 5
Agora só falta usar as reatâncias e a frequência angular para achar e :