Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 99

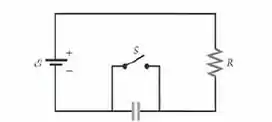
No circuito da figura abaixo, a fem é igual a 6,00 V e a resistência interna é desprezível. A capacitância é igual a 1,50   μ F e a resistência é igual a 2,00   M Ω . A chave S ficou fechada por um longo tempo. A chave S é aberta. Depois de um intervalo de tempo igual a uma constante de tempo do circuito, determine (a) e a carga na placa da direita do capacitor, (b) a taxa na qual a carga está aumentando, (c) a corrente, (d) a potência fornecida pela bateria, (e) a potência entregue ao resistor e (f) a taxa na qual a energia armazenada no capacitor está aumentando.

Passo 1

Fala galera, bom dia/boa tarde/boa noite, essa questão é um pouco extensa, mas nada que não consigamos desenrolar, só cola em mim que é sucesso!

Primeiramente, teríamos que encontrar a carga no capacitor em t =   τ e diferenciar a expressão em relação ao tempo para encontrar a taxa na qual a carga está aumentando (corrente). A potencia fornecida pela bateria é dada pela fração entre a corrente e a fem e a potencia entregue ao resistor pode ser calculada pela resistência multiplicada pela corrente ao quadrado. Por ultimo (mas não menos importante), para achar a taxa na qual a energia armazenada no capacitor está aumentando; Basta derivar em t =   τ a razão entre a função da carga ao quadrado em função do tempo e o dobro da capacitância. Se você não conhece nenhuma das equações que foram citadas, recomendo fortemente que revise o conteúdo de corrente elétrica e circuitos de corrente direta aqui no Responde aí!

Dito isto, usaremos as seguintes equações:

Q t =   C   ℇ   ( 1 - e - t / τ )   (1)

P τ = I τ   ℇ (2)

P R , τ = I τ 2   R (3)

U t = Q 2 t 2 C (4)

SUSTENTE CALCULO AGORA!

Passo 2

Primeiramente, vamos iniciar pela alternativa (a), basta utilizar a equação 1 em t =   τ para substituir as variáveis pelos dados estabelecidos na questão:

Q t =   C   ℇ   ( 1 - e - t / τ )

Q τ = 1.50   μ F ( 6.00   V )   ( 1 - e - τ / τ )

Q τ = 1.50   μ F ( 6.00   V )   ( 1 - e - 1 )

Q τ = 5.689   μ C

Fácil, fácil, hein, hein, vamos para a próxima!

Passo 3

Para a alternativa (b) e (c) usaremos a equação 1, começaremos diferenciando-a:

d Q t d t =   I t =   I 0 e - t / τ

A derivada da função que representa a carga em relação ao tempo é a corrente elétrica, feito isto, vamos aplicar a Lei de Kirchhoff no circuito para encontrar uma expressão para I 0 :

ℇ - R   I 0 -   V C 0 = 0

Por conta de V C 0 = 0 , temos:

ℇ - R   I 0 = 0

ℇ = R   I 0

  I 0 =   ℇ R

Para a alternativa (b), basta substituir isto na derivada da equação 1, pata termos nossa resposta:

d Q t d t =   I t =   ℇ R e - t / τ

Para a alternativa (c), basta aplicar t =   τ e substituindo as variáveis pelos termos estabelecidos na questão, temos:

I τ =   ℇ R e - τ / τ

I τ =   ( 6.00   V ) ( 2.00   M Ω ) e - 1

I τ =   1.104   μ C / s

I τ =   1.10   μ C / s

Prontinho, dois coelhos com uma cajadada só!

Passo 4

Para a alternativa (d) e (e) basta utilizar os dados estabelecidos na questão e na alternativa anterior (c) nas equações 2 e 3:

Alternativa (d):

P τ = I τ   ℇ

P τ = ( 1.104   μ A ) ( 6.00   V )

P τ = 6.62   μ W

Alternativa (e):

P R , τ = I τ 2   R

P R , τ = 1.104   μ A 2   ( 2.00   M Ω )

P R , τ = 2.44   μ W

PRONTINHO, agora vamos para a última alternativa (Tensão aumenta)

Passo 5

Para a alternativa (f), basta derivar a equação 4, aplicar t =   τ e substituir as variáveis pelos valores dados na questão:

U t = Q 2 t 2 C

d U t d t = 1 2 C d d t [ Q 2 t ]

d U t d t = 1 2 C ( 2 Q ( t ) ) d Q ( t ) d t

d U t d t = Q t C I ( t )

d U τ d t = Q τ C I ( τ )

d U τ d t = 5.689   μ C 1.50   μ F 1.104   μ A

d U τ d t = 4.19 μ W

PRONTINHO, Bons estudos, fica bem!

Resposta

(a) Q τ = 5.689   μ C

(b) d Q t d t =   I t =   ℇ R e - t / τ

(c) I τ =   1.10   μ C / s

(d) P τ = 6.62   μ W

(e) P R , τ = 2.44   μ W

(f) d U τ d t = 4.19 μ W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Dar apoio à afirmação de que um condensador com fugas (para o qual a resistência do dielétrico é finita) pode ser modelado como um condensador que tem uma resistência infinita em paralelo com uma
A figura 25-77 mostra a base do circuito de varrimento utilizado num osciloscópio. O interruptor S é um interruptor electrónico que fecha sempre que o potencial através do interruptor S aumenta para u
No circuito mostrado na Figura 25-78, R 1 = 2,00M Ω , R 2 = 5,00M Ω , e C = 1,00μ F . O capacitor está inicialmente sem carga em ambas as placas. Em t= 0, a chave S é fechada e, em t= 2,00 s, a chave
O capacitor na Figura 25-49 está inicialmente descarregado. A chave S está fechada e permanece fechada por um longo tempo. Durante este tempo, (a) a energia fornecida pela bateria é 1 2 C ε 2 , (b) a
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas