Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 85
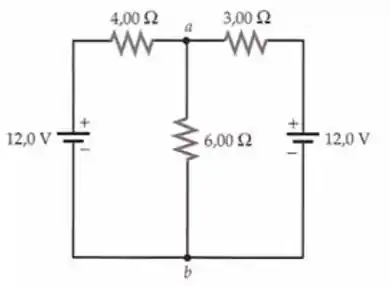
No circuito mostrado na Figura 25-62, as baterias têm resistência interna insignificante. Encontre (a) a corrente em cada ramal do circuito, (b) a diferença de potencial entre o ponto a e o ponto b, e (c) a energia fornecida por cada bateria.
Passo 1
Eae galera! Tudo tranquilo? Tendo uma visão geral da coisa, seja I1 a corrente fornecida pela bateria esquerda, I2 a corrente fornecida pela bateria direita e I3 a corrente através do resistor de 6,00 Ω, direcionado para baixo. Podemos aplicar as regras de Kirchhoff para obter três equações que podemos resolver simultaneamente para I1, I2 e I3.
Passo 2
Vamo lá. (a) Aplique a regra de junção de Kirchhoff na junção a:
Aplique a regra de loop de Kirchhoff a um loop ao redor do lado externo do circuito para obter:
Aplique a regra de loop de Kirchhoff a um loop em torno do ramo esquerdo do circuito para obter:
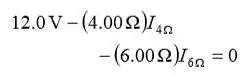
Substituindo a primeira equação nessa última:
Dessa forma, chegamos no sistema:
Multiplicando a primeira equação por :
Somando as duas equações:
Opa! E para achar , só precisamos substituir esse valor em qualquer uma das equações do sistema que tínhamos. Vamos substituir na primeira equação:
E, por último, sabemos que:
Dessa forma:
Passo 3
(b) Aplique a lei de Ohm para encontrar a diferença de potencial entre os pontos a e b:
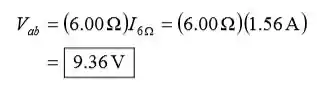
(c) Expresse a energia fornecida pela bateria de 12,0 V no ramo esquerdo do circuito:
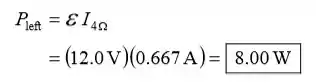
Passo 4
Para a bateria da direita, teremos que a potência é: