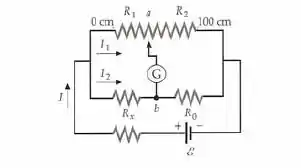
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência é conhecida. Esta “ponte” PE usada para determinar o valor de uma resistência desconhecida . As resistências e consistem em um fio de de comprimento. O ponto a é um contato deslizante que se move ao longo do fio para variar resistências. A resistência é proporcional à distância da extremidade esquerda do fio (identificada como ao ponto a, e é proporcional à distância do ponto a até a extremidade do fio (identificada como ). A soma de e permanece constante. Quando os pontos a e b estão no mesmo potencial, não há corrente no galvanômetro e dizemos que a ponte está equilibrada. (Como o galvanômetro é usado para detectar a ausência de corrente, ele é chamado de detector nulo.) Se a resistência fixa , determine o valor da resistência desconhecida se (a) a ponte é equilibrada na marca de , (b) a ponte é equilibrada na marca de , (c) a ponte é equilibrada na marca .

Aplicando a Segunda Lei de Kirchhoff’s nas duas malhas, temos:

(2)

(3)

Quando a ponta está balanceada, , aplicando isso nas equações (2) e (3), teremos:

(4)

(5)

Se dividirmos a equação (4) pela (5), temos que:

(6)

Expressando e pela equação (1), teremos:

(7)

Agora, com a equação (7) podemos responder todas as alternativas! Sigam-me os bons!

Para a alternativa (a), se a ponte é equilibrada na marca de , então , :

Para a alternativa (b), se a ponte é equilibrada na marca de , então , :

Para a alternativa (c), se a ponte é equilibrada na marca de , então , :

PRONTINHO, questão respondida com sucesso, Até a próxima pae