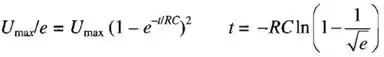Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 86
Um circuito possui um constante de tempo . (a)Quando o circuito está descarregadp, quanto tempo levará para a emergoa ar,azemada ser redizoda a do seu valor inicial? (b)Quando ele está carregando, quanto tempo levará para a energia armazenada atingir do seu valor máximo?
Passo 1
A energia muda exponencialmente, mas isso não obedece exatamente a mesma equação da carga que é proporcial ao o quadrado da carga. Para as fórmulas temos que:
Para reduzir a energia para do valor inicial, (a)temos:
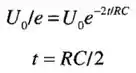
Passo 2
Para a descarga, temos que (b):
Para chegar a da energia máxima,
Resposta
Exercícios de Livros Relacionados
Um resistor com R = 850Ω é conectado com as placas de um capacitor carregado, cuja capacitância é dada por C = 4,62μ F . Imediatamente antes de a conexão ser feita, a carga no capacitor é igual a 8,10
Usando a equação (26.17) para a corrente durante o processo de descarga do capacitor, deduza uma expressão para a potência instantânea P = i 2 R no resistor. (b)Integre a expressão de P para calcular
A corrente no processo de carga de um capacitor é dada pela Equação (26.13). (a)A potência instantânea fornecida pela bateria é igual a ε i . Integre essa expressão para calcular a energia total forne
Estritamente falando, a equação (26.16) mostra que seria necessário um tempo infinito para descarregar completamente um capacitor. Contudo, na prática, podemos considerar um capacitor completamente de