Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 87
A corrente no processo de carga de um capacitor é dada pela Equação (26.13). (a)A potência instantânea fornecida pela bateria é igual a . Integre essa expressão para calcular a energia total fornecida pela bateria. (b)A potência total dissipada no resistor é igual a . Integre essa expressão para calcular a energia total dissipada no resistor. (c)Calcule a energia final armazenada no capactiro e mostre que ela é igual à energia total fornecida pela bateria menos a energia dissipada no resistor, obtidas nos itens (a) e (b). (d)Que fração da energia fornecida pela bateria é armazenada no capacitor? Como essa fração depende de ?
Passo 1
Para os itens (a) e (b) vamos evaluar as integrais como especificado nesse problema. A corrente como função do tempo é dada pela eq. (26.13):
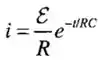
A energia armazenada no capacitor é dada por:
Passo 2
Então vamo lá né! Para o item (a), temos que:
A energia total da bateria é:
(b) Temos:
A energia total dissipada no resistor é:
Passo 3
A carga final no capacitor é dada por:
A energia armazenada é:
A energia final armazenada no capacitor é:
E subtraímos isso pela energia dissipada no resistor.
Para o item (d), temos que da energia dada pela bateria é armazenada no capacitor. Essa fração é independente do . A outra da energia dada pela bateria é dissipada no resistor. Quando é pequeno, a corrente inicalmente é alta mas morre rapidamente. Quando é alta, a corrente é menor mas dura mais.