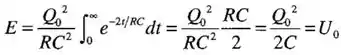Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 88
Usando a equação (26.17) para a corrente durante o processo de descarga do capacitor, deduza uma expressão para a potência instantânea no resistor. (b)Integre a expressão de para calcular a energia total dissipada no resistor e mostre que ela é igual à energia total armazenada inicalmente no capacitor.
Passo 1
Vamos primeiro identificar que:
A energia armazenada num capacitor que:
E a corrente:
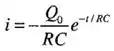
Passo 2
Executando, temos que:
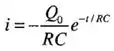
Nos dá que:
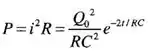
Logo:
Resposta
Exercícios de Livros Relacionados
Um capacitor de alarme contra roubo. A capacitância de um capacitor pode ser alterada por um material dielétrico que, embora fora do capacitor, esteja suficientemente próximo do capacitor para ser pol
72- O capacitor indicado na Figura 26.74 está inicialmente descarregado. A chave está fechada no instante t = 0 . ( a ) Imediatamente após a chave ser fechada, qual é a corrente que passa através de c
A chave S da Fig. 27-63 é fechada no instante t = 0 ,fazendo om que um capacitor inicialmente descarregado de capacitância C = 15,0 μ F comece a se carregar através de um resistor de resiscência R = 2
Os capacitores C 1 e C 2 estão conectados a um resistor de resistência R e a uma bateria ideal que tem tensão nos terminais V 0 , como mostra a Figura 25-79. A chave S está inicialmente no contato a e
(a) Dar apoio à afirmação de que um condensador com fugas (para o qual a resistência do dielétrico é finita) pode ser modelado como um condensador que tem uma resistência infinita em paralelo com uma