Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 5

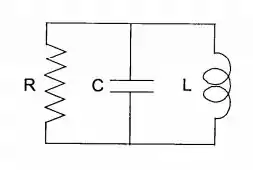
No circuito RLC em paralelo (figura), (a) Calcule a frequência angular ω 0 das oscilações livres e a constante de amortecimento γ . (b) Para R = 10 k Ω , C = 1   μ F , L = 10   m H , qual é o valor de ω 0 ? Depois quantos períodos a energia eletromagnética se reduz à metade do seu valor inicial?

Passo 1

Para resolvermos, vamos utilizar as leis de Kirchoff para circuitos em paralelo, somando as tensões de todo o sistema. Com isso, vamos encontrar nossa corrente que passa pelo capacitor, resistência e pelo nosso indutor, aí aplicaremos as seguintes relações

I R t = V t R ,     I L = 1 L ⋅ ∫ V t d t ,     I C = C ⋅ d V t d t

Para encontrarmos a equação que rege nosso oscilador.

Passo 2

  1. Pra encontrarmos a equação que rege nosso sistema, vamos precisar aplicar a lei de Kirchoff. Como nesse caso as correntes no sistema são todas diferentes, vamos calcular pela tensão que se mantem constante em todo o sistema.

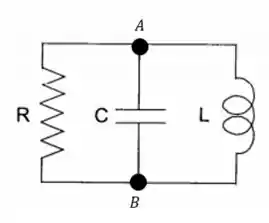
    2. Se usarmos a lei de Kirchoff nos pontos A e B , vamos chegar que nossas correntes respeitam a seguinte relação:

    I R + I L + I C = 0

    Se substituirmos as relações dadas no passo 1, vamos ter que:

    V t R + 1 L ⋅ ∫ V t d t + C ⋅ d V t d t = 0

    Se derivarmos toda a relação, vamos chegar que

    1 L ⋅ V t + 1 R ⋅ d V t d t + C ⋅ d 2 V t d t 2 = 0

    d 2 V t d t 2 + 1 R C ⋅ d V t d t + 1 L C ⋅ V t = 0

    Chamando ω 0 = 1 L c e γ = 1 R C , vamos ter que

    d 2 V t d t 2 + γ ⋅ d V t d t + ω 0 2 ⋅ V t = 0

    Porém, temos que essa é nossa oscilação natural. Nossa oscilação livre, como mostrado no capítulo, é dada por ω 1 = ω o 2 - γ 2 4 = 1 L C - 1 4 R 2 C 2 .

    Passo 3

  2. Substituindo os valores dados no enunciado em ω 1 e γ , vamos ter que:

ω 1 = 1 L C - 1 4 R 2 C 2 = 1 10   m H ⋅ 1   μ F - 1 4 ⋅ 10   k Ω 2 ⋅ 1   μ F 2 = 10 4 H z

Resposta

  1. ω 1 = 1 L C - 1 4 R 2 C 2 ,     γ = 1 R C
  2. 10 4   H z ; 11   p e r í o d o s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um circuito R L C série é alimentado de tal forma que a tensão máxima no indutor é 1,50 vez a tensão máxima no capacitor e 2,00 vezes a tensão máxima no resistor. (a) Qual é o ϕ do circuito? (b) o cir
No caso de um circuito R L C série, mostre que em um ciclo completo de período T (a) a energia armazenada no capacitor não varia; (b) a energia armazenada no indutor não varia; (c) a energia fornecida
(a) Em um circuito L C oscilante, qual é a carga, em termos da carga máxima Q do capacitor, quando a energia do campo elétrico é 50,0 % de energia do campo magnético? (b) Que fração do período deve tr
Um circuito LC oscilante é formado por um indutor de 75,0 m H e um capacitor de 3,60 μ F Se a carga máxima do capacitor é 2,90 μ C , determine (a) a energia total presente no circuito e (b) a corrente
Em um circuito LC oscilante, a energia total é convertida de energia elétrica no capacitor em energia magnética no indutor em 1,50 μ s . Determine (a) o período das oscilações e (b) a frequência das o