Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 3- Ed: 4º - Capítulo 35.Exercícios e Problemas - Ex. 16

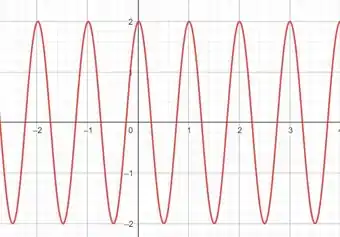
Um circuito LC tem uma indutância de 3,00 mH e uma capacitância de 10,0 μ F Calcular (a) a frequência angular e ( b) o período de oscilação.(c) No instante t — 0. a carga do capacitor é de 200 μ C e a corrente é zero. Desenhe aproximadamente o gráfico da carga do capacitor em função do tempo.

Passo 1

Eae galera!! Tudo bom? Vem comigo para mais um exercício.

  1. Vamos usar a formula da frequência angular,

    2. ω = 1 L C

    ω = 1 ( 3 ⋅ 10 - 3 ) ( 10 - 5 )

    ω = 5,77 ⋅ 10 3   r a d / s

    Passo 2

  2. Vamos usar a equação da velocidade angular lá da cinemática,

    3. T = 2 π ω

    T = 2 π 5,77 ⋅ 10 3

    T = 1,09   m s

    Passo 3

  3. Utilizando o Geogebra, e tomando na escala, 200   μ C = 2 ,

Bora pro próximo.

Resposta

  1. ω = 5,77 ⋅ 10 3   r a d / s .
  2. T = 1,09   m s

Exercícios de Livros Relacionados

74. Na Figura 30.32 , a chave é fechada, com o capacitor contendo a polaridade indicada. Determine o sentido (horário ou anti-horário) da corrente induzida na espira retangular A .
66. No circuito indicado na Figura 30.26 , a chave S está fechada há um longo tempo, o suficiente para que a leitura da corrente esteja estacionária a 3,50A . Subitamente, a chave S 2 é fechada, e a c
64. No circuito indicado na Figura 30.24 , a bateria e o indutor não possuem resistência interna significativa e não há corrente no circuito. Após a chave ser fechada, determine as leituras do amperím
70. Depois que a corrente na Figura 30.28 atinge seu valor estacionário final com a chave S 1 fechada e a chave S 2 aberta, a chave S 2 é fechada, colocando o indutor em curto-circuito. (A chave S 1 p
69. Considere o circuito indicado na Figura 30.28 . Seja ε = 36,0V , R 0 = 50,0Ω , R = 150,0Ω e L = 4,0H . ( a ) A chave S 1 é fechada e a chave S 2 é mantida aberta. Logo depois que a chave S 1 é fec