69. Considere o circuito indicado na Figura . Seja , , e . A chave é fechada e a chave é mantida aberta. Logo depois que a chave é fechada, quais são os valores da corrente que passa em da diferença de potencial e da diferença de potencial de ? Depois que a chave é fechada durante um tempo muito longo (mantendo a chave aberta), de modo que a corrente atinja seu valor estacionário final, quais são os valores de , e ? Determine as expressões de e em função do tempo, a partir do momento em que a chave é fechada. Seu resultado deve estar de acordo com item , quando , e com a resposta do item , quando . Faça um gráfico de , e em função do tempo.

Vamos começar com o item , sabemos o comportamento de em relação ao tempo dada por:

Logo depois que a chave é fechada temos , assim temos que:

Para achar a diferença de potencial vamos usar a lei de Ohm, temos que:

E segundo a lei das malhas temos que:

Sabemos os valores de e , então:

Agora vamos discutir o item , o longo tempo que o enunciado fala pode ser interpretado como , então usando isso na nossa fórmula para , temos:

O termo da exponencial vai a zero então:

Sabendo disso o potencial pode ser tirado da lei de Ohm, assim:

Usando a lei das malhas de noto, temos que:

Sabemos os valores de e , então:

Bem, o item pede uma expressão para a corrente em função do tempo e isso já tínhamos encontrado no passo , que é:

Agora para e temos que achar, mais acima através da lei de Ohm e da lei das malhas, encontramos que:

Substituindo a fórmula de na primeira expressão temos:

Assim, a nossa segunda expressão mais acima fica da seguinte maneira:

Agora vamos ver se essas fórmulas batem com o que encontramos no item para e para o item para .

Primeiro para , temos:

Agora para :

Agora para :

Vamos ver para o caso de , temos:

Agora para :

Agora para :

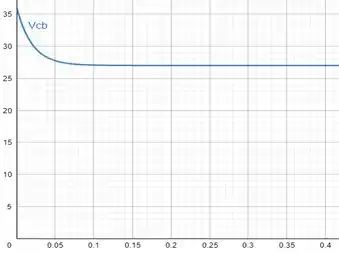
Os gráficos das funções de , e , estão mostrados abaixo.

Para temos:

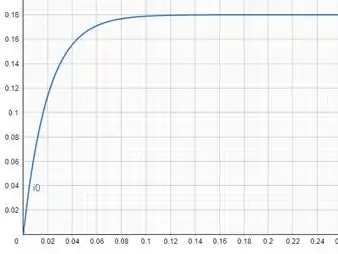
Para , temos:

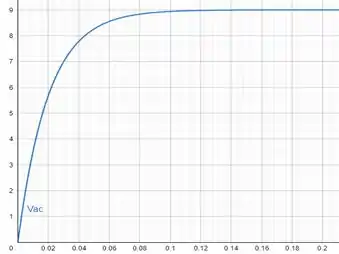
Para , temos: