Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 22
Um feixe de prótons, movendo-se ao longo de uma direção tomada como eixo , com velocidade de , penetra numa região onde existe um campo magnético uniforme de intensidade 100 gauss, dirigido ao longo do eixo . Calcule a deflexão do feixe na direção y, após penetrar uma distância de 50 cm ao longo da direção x na região onde existe campo magnético.
Passo 1
Como a direção da força depende do produto vetorial entre v e B, pela regra da mão direita ela aponta para baixo no eixo y, gerando uma trajetória circular de raio R. Lets bora calcular o raio da trajetória.
Passo 2
Agora que descobrimos o raio vamos fazer um esboço para visualizar a situação
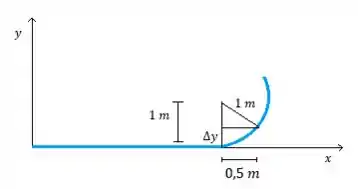
Aqui a linha azul é a trajetória do feixe de prótons. Quando são submetidos ao campo magnético começam a percorrer uma trajetória circular que calculamos o raio.
Para calcular nossa deflexão basta calcular aquele cateto vertical do triângulo e subtrair do raio, show? Fica assim