Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 126
Um coelho assustado, que está se movendo a na direção leste, penetra em uma grande área plana de gelo com atrito desprezível. Enquanto o coelho desliza no gelo e a força do vento faz com que ele adquira uma aceleração constante de na direção norte. Escolha um sistema de coordenadas com a origem na posição inicial do coelho sobre o gelo e o sentido positivo do eixo apontando para leste. Em termos dos vetores unitários quas são (a) a velocidade e (b) a posição do coleho após ter deslizado por ?
Passo 1
Vamos começar com um desenho da situação. A aceleração do coelho tem que apontar par ao norte e a velocidade para o leste:
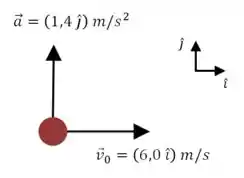
E nosso primeiro objetivo é encontrar a velocidade após . Para fazer isso, precisamos de alguma fórmula que dê a velocidade como função do tempo:
Agora é só substituir os valores que conhecemos:
Passo 2
(b) Nosso próximo objetivo é descobrir a posição do coelho após esse mesmo intervalo de tempo.
Vamos lembrar da fórmula que dá a posição como função do tempo, tomando como ponto inicial o instante que está representado no desenho:
Mais uma vez, podemos substiuir os valores para calcular quanto :
Resposta
(a) .
(b) .