Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 4.Problemas Adicionais - Ex. 123
No exemplo 4-7b uma bala é disparada por um canhão situado ao nível do mar com um ângulo de com a horizontal e atinge uma distância de . Qual seria o aumento da distância atingida pela bala se o canhão estivesse a uma altura de ?
Passo 1
Nosso objetivo é encontrar a distância horizontal percorrida pela bala até ela atingir o chão. Mas com uma complicação, o canhão está em uma posição elevada. Vamos dar uma olhada no desenho:
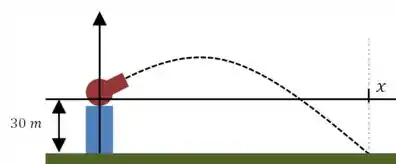
A equação que dá a trajetória da bola é a seguinte:
Nesse desenho nós colocamos a origem do sistema de coordenadas na posição inicial da bala, então, nosso objetivo é encontrar o valor de quando .
Passo 2
O enunciado já deu o ângulo de lançamento , e no exemplo mencionado vemos que .
Com esses valores, podemos resolver aquela equação do segundo grau para encontrar .
Então, aplicando a fórmula de Bháskara:
E nesse caso só uma raiz positiva pode fazer sentido, então:
Passo 3
No exemplo mencionado no enunciado, quando o canhão estava na altura do solo, era:
Ou seja, o aumento na distância horizontal foi:
Resposta
O aumento na distância atingida foi de metros.