Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 6.Problemas - Ex. 6
A condutividade de um cilindro de comprimento e área transversal cresce linearmente com a distância, assumindo o valor numa extremidade e na outra. Calcule a resistência total do cilindro.
Passo 1
A imagem a seguir ilustra a condutividade.
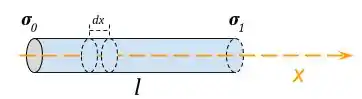
Como ele diz que a condutividade cresce linearmente, temos que
Repare no gráfico dessa função! Com ela podemos achar o e o .
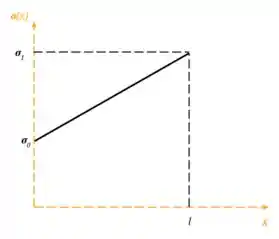
Sendo
Passo 2
A variação infinitesimal da resistência com relação a posição pode ser escrita como
Substituindo o , teremos
Agora só precisamos integrar esse no intervalo de a .
Passo 3
Galera essa integral pode ser resolvida usando uma substituição simples.
Usando uma substituição simples, temos
Logo
Pronto. Acabamos!
Resposta
Exercícios de Livros Relacionados
A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo
Seguindo o procedimento análogo ao do 20.6P, calcule a constante de tempo de um capacitor esférico preenchido por um dielétrico.
A Figura 20.11 mostra um cubo de sílica de aresta igual a 3,0c m . Sobre duas faces opostas são depositados filmes espessos de metal, e uma terceira face recebe um filme de ouro com espessura de apena
O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta em correntes não-nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor d
A Figura 20.15 mostra uma ponte de resistência, circuito amplamente utilizado para medida de resistências elétricas. R 1 e R 2 de valor fixo, R V é uma resistência de valor continuamente sintonizável