Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 20.Exercícios e Problemas - Ex. 3

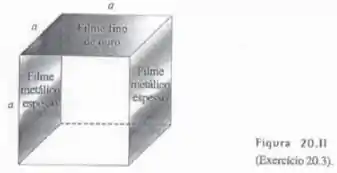
A Figura 20.11 mostra um cubo de sílica de aresta igual a 3,0   c m . Sobre duas faces opostas são depositados filmes espessos de metal, e uma terceira face recebe um filme de ouro com espessura de apenas 1,0 ⋅ 10 - 6   c m . Uma voltagem de 1,0   m V é aplicada entra as faces metalizadas com filmes espessos. Calcule a corrente (a) no filme de ouro; (b) no bloco de sílica.

Passo 1

No desenho a seguir a seta representa o sentido da corrente no sistema:

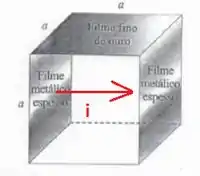
Podemos encarar esse sistema como dois resistores em paralelo: um que é o cubo de sílica e o outro que é filme fino de ouro. Vamos calcular a resistência de cada um!

Para o cubo de sílica, temos que

R s i l i c a = ρ s i l i c a L A

Como L = a e A = L 2 , temos que

R s l i l i c a = ρ s i l i c a a a 2 = ρ s i l i c a a

Na tabela da página 83 do livro, achamos ρ s i l i c a = 7,5 ⋅ 10 17   Ω m , de modo que

R s i l i c a = 7,5 ⋅ 10 17   Ω m 3,0 ⋅ 10 - 2   m = 2,5 ⋅ 10 19   Ω

Já para o filme de ouro:

R o u r o = ρ o u r o a a d = ρ o u r o d

Na tabela achamos ρ o u r o = 2,25 ⋅ 10 - 8   Ω m e a espessura do filme d = 1,0 ⋅ 10 - 8   m , de modo que

R o u r o = 2,25 ⋅ 10 - 8   Ω m 1,0 ⋅ 10 - 8   m = 2,25   Ω

Passo 2

Para dois resistores em paralelo, temos que

V = R o u r o I o u r o = R s i l i c a I s i l i c a

Com isso,

I o u r o = V R o u r o = 1,0 ⋅ 10 - 3 2,25 → I o u r o = 4,4 ⋅ 10 - 4   A

I s i l i c a = V R s i l i c a = 1,0 ⋅ 10 - 3 2,5 ⋅ 10 19 → I s i l i c a = 4,0 ⋅ 10 - 23   A

Resposta

I o u r o = 4,4 ⋅ 10 - 4   A

I s i l i c a = 4,0 ⋅ 10 - 23   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura 20.12 mostra um capacitor cilíndrico preenchido por um material dielétrico de resistividade elétrica ρ e constante dielétrica κ . Uma bateria aplica uma voltagem V ao capacitor.a) Calcule a c
O cubo visto na Figura 20.10 tem duas faces metalizadas. O material do cubo tem resistividade ρ muito maior que a do metal. Calcule a resistência elétrica entre as faces metalizadas.
A Figura 20.13 mostra um cone feito de material com resistividade ρ , com a ponta aparada por um plano paralelo à base. As duas faces circulares do corpo têm raios a e b , e forma metalizadas. Supondo
Seguindo o procedimento análogo ao do 20.6P, calcule a constante de tempo de um capacitor esférico preenchido por um dielétrico.