Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 12.1 - Ex. 12
Considerando os torques em relação à articulação de seus ombros, estime a força que seus músculos deltoides (os músculos no topo de seus ombros) devem exercer sobre seu braço para mantê-lo estendido no nível do ombro. Depois, estime a força que eles devem exercer quando você segura um peso de à distância do braço estendido.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Na imagem abaixo está representado o diagrama de corpo livre do sistema:
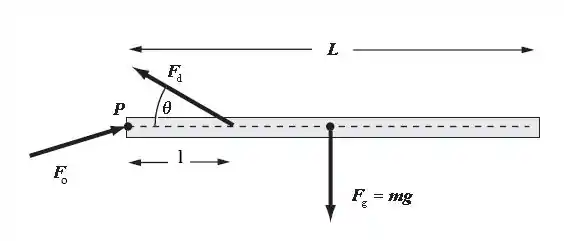
Aplicando , temos:
Passo 2
Agora vamos imaginar a situação em que seguramos no final do braço. Nossas equações ficariam assim:
Resposta
Exercícios de Livros Relacionados
As forças F 1 , F 2 e F 3 agem sobre a estrutura cuja vista superior aparece na figura. Deseja-se colocar a estrutura em equilíbrio aplicando uma quarta força em um ponto como P . A quarta força tem c
Sua muleta é pressionada contra a calçada por uma força F → c ao longo de sua própria direção, como na Figura 12-29. Esta força é equilibrada pela força normal F → n e por uma força de atrito f → s .
As pernas de um tripé formam ângulos iguais de 90° entre si no vértice, onde elas se juntam. Um bloco de 100 kg está pendurado no vértice. Quais são as forças de compressão sobre as três pernas?
Uma partícula é submetida a forças dadas, em newtons, por F → 1 = 8,40i ^ - 5,70j ^ e F → 2 = 16,0i ^ + 4,10j ^ . (a) Qual é a componente x e (b) Qual é a componente y da força F → 3 que equilibra a r
Um alçapão quadrado em um teto tem 0,91m de lado, uma massa de 11k g e está preso por uma dobradiça de um lado e por um ferrolho do lado oposto. Se o centro de gravidade do alçapão está a 10c m do cen