Uma partícula é submetida a forças dadas, em newtons, por e . (a) Qual é a componente e (b) Qual é a componente da força que equilibra a resultante das forças e ? (c) Qual é o ângulo da força com o semieixo positivo?

Se a força equilibra a resultante de e , então:

(a) Então, a componente da força é .

(b) E a componente da força é .

Para calcular o ângulo que a força forma com o semieixo positivo, vamos dar uma olhada nesse desenho:

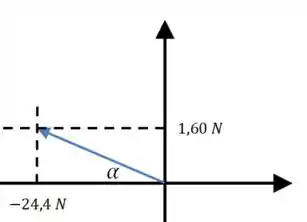
Se contarmos o ângulo a partir do semieixo negativo, ficaremos com o seguinte:

E podemos simplismente adicionar um sinal negativo para corrigir a diferença, já que o enunciado pediu para calcularmos o ângulo a partir do semieixo positivo.