Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 61

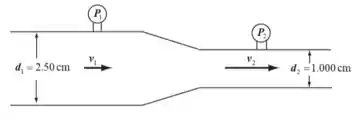
Considera-se uma tubulação horizontal flexível para transportar água (ilustrada acima).

É necessária uma vazão mínima I v = 0,050 L / s . O tubo tem uma secção transversal circular de raio r 2 = 0,5 c m e outra de raio r 1 = 1,25 c m .

Coloca-se dois sensores de pressão P 1 e P 2 para medir as respectivas pressões das duas áreas distintas.

Os técnicos do laboratório informam que se a vazão cair para menos que 0,050 L/s o sistema pode sofrer superaquecimento e danificar-se, então é necessário programar um alarme que indique quando a vazão está abaixo desse valor.

Qual será a diferença de pressão crítica que devemos programar os sensores para enviar o alarme? É uma diferença de pressão mínima ou máxima?

Suponha um fluxo laminar não viscoso em estado estacionário.

Passo 1

Iremos usar a equação de Bernoulli para achar as relações de P 1 e P 2 :

P 1 + p g h 1 + 1 2 p v 1 2 = P 2 + p g h 2 + 1 2 p v 2 2

Notem que a questão nos informa que ambas as extremidades estão à mesma altura, portanto podemos cancelar a expressão p g h de ambos os lados da equação e passamos a ter:

P 1 + 1 2 p v 1 2 = P 2 + 1 2 p v 2 2

Como queremos a diferença de pressão, vamos encontrar a relação P 1 - P 2 :

P 1 - P 2 = 1 2 p v 2 2 - 1 2 p v 1 2

P 1 - P 2 = 1 2 p ( v 2 2 - v 1 2 )

Notem que ainda temos muitas variáveis, vamos tentar eliminar v 1 e v 2 , para isso, vamos transformar a expressão em uma fração, para podermos aplicar a equação da continuidade:

P 1 - P 2 = 1 2 p v 1 2 ( v 2 2 v 1 2 - 1 )

P 1 - P 2 = 1 2 p v 1 2 ( v 2 v 1 2 - 1 )

Passo 2

Agora iremos aplicar a equação da continuidade que nos garante que:

A 1 v 1 = A 2 v 2

v 2 v 1 = A 1 A 2 = π r 1 2 π r 2 2

Lembrando que: r = d 2

v 2 v 1 = π d 1 2 4 π d 2 2 4 = d 1 2 d 2 2

v 2 v 1 = d 1 d 2 2

Passo 3

Pela definição de vazão, temos que:

I v = A v

Logo:

v 1 = I v A 1 = I v π d 1 2 4

v 1 = 4 I v π d 1 2

Passo 4

Por último, vamos entrelaçar as equações encontradas:

P 1 - P 2 = 1 2 p v 1 2 ( v 2 v 1 2 - 1 )

v 2 v 1 = d 1 d 2 2

v 1 = 4 I v π d 1 2

Logo, teremos que:

P 1 - P 2 = 1 2 p 4 I v π d 1 2 2 ( d 1 d 2 2 2 - 1 )

P 1 - P 2 = 1 2 p 4 I v π d 1 2 2 ( d 1 d 2 4 - 1 )

Lembrando que:

p = 1.10 3 k g / m 3 (densidade da água).

1 L = 0,001 m 3

Agora, vamos substituir os valores fornecidos pela questão:

P 1 - P 2 = 1 2 p 4 I v π d 1 2 2 ( d 1 d 2 4 - 1 )

P 1 - P 2 = 1 2 ( 1.10 3 ) 4.5 . 10 - 5 π 0,025 2 2 ( 2,50 1,00 4 - 1 )

P 1 - P 2 = 196,02 P a

P 1 - P 2 = 0,2 k P a

Passo 5

Definindo P 1 - P 2 = ∆ P e ao compararmos:

∆ P = 1 2 p 4 I v π d 1 2 2 ( d 1 d 2 4 - 1 )

Percebemos que ∆ P ∝ I v 2 (leia ∆ P diretamente proporcional a I v 2 ) e como sabemos, as funções do tipo f x = + x 2 (dado um x qualquer) tem comportamento ilustrado abaixo:

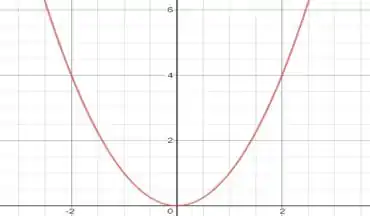
Portanto, se ∆ P ∝ I v 2 , então P 1 - P 2 terá uma diferença de pressão mínima.

Resposta

∆ P = 0,2 k P a e será uma diferença de pressão mínima

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo horizontal se estreita de um diâmetro de 10 cm, na localização A, para um diâmetro de 5 cm, na localização B. Para um fluido incompressível e não-viscoso que escoa sem turbulência de A para B,
Um tubo horizontal se estreita de um diâmetro de 10 cm, na localização A, para um diâmetro de 5 cm, na localização B. Para um fluido incompressível e não-viscoso que escoa sem turbulência de A para B,
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
Um pequeno orifício circular com diâmetro igual a 6,0mm é cortado na superfície lateral de um grande tanque de água , a uma profundidade de 14,0m abaixo da superfície da água, a uma profundidade de 14
Qual é a pressão manométrica necessária no tubo principal da rua para que uma mangueira de incendico ligada a ela seja capaz de lançar água até uma altura de 15,0m? (Suponha que o diâmetro do tubo pri