Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 50
Um copo de 1,00 kg contendo 2,00 kg de água repousa em uma balança. Um bloco de alumínio de 2,00 kg (densidade de ) suspenso de uma balança de mola está submerso na água, como na Figura abaixo. Encontre as leituras de ambas as escalas.
Passo 1
Beleza gente, sem pânico!! A gente quer a leitura da balança suspensa e da balança de baixo. Vamos primeiro achar a leitura de uma e dai jogar na equação da outra... parte por parte tudo dá certo!
A leitura da balança de cima reflete o equilíbrio de forças no bloco, já na balança de baixo, o equiíbrio de forças do conjunto bloco+água+copo.
Primeiro, temos que:
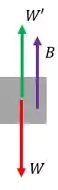
A leitura da balança suspensa , W’, é a tensão na corda da balança, por isso ela vai ser a diferença entre o peso próprio do bloco de alumínio W e a força flutuante que atua sobre ele para cima.
A gente chama esse de peso aparente do bloco, porque é o carga final que a balança de cima deve suportar, para que haja equilíbrio.
Já a leitura da balança de baixo vamos entender assim: A balança mede a Normal, certo? E qual Normal? É a Normal entre o copo com água e a balança. Vamos fazer o diagrama de corpo livre desse sistema água+copo
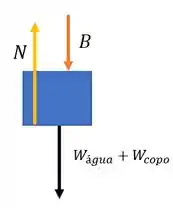
Ué?!?!?!?! Empuxo apontando para baixo?! Pode isso?
A regra é clara! Se tem um empuxo sobre o bloco de alumínio produzido pela água, pela terceira lei de Newton, tem que ter uma força de reação com mesma intensidade, só que no sentido oposto!
Ah tá! Então esse empuxo pra baixo é a reação do bloco sobre o liquido! Beleza, então! Segue jogo! Já o peso do bloco não gera reação na água porque a água não suporta esse peso.
Então usando a condição de equilíbrio, sendo a leitura da balança de baixo:
A ideia é a gente usar os dados que nos deram e as massas específicas que encontamos na tabela 13-1 para achar e depois . Vamos!
Passo 2
Temos
O peso do bloco é
nós achamos pelo teorema de Arquimedes. Como o bloco está completamente submerso na água, podemos dizer que é
Agora expressamos esse volume do bloco, em termos da densidade do alumínio!!
Substituindo em :
Passo 3
Subsituinto essas coisas na nossa equação de
Pela tabela 13-1:
Aplicando os valores numéricos do enunciado e esses valores tabelados na nossa expressão de
E temos a leitura da balança de cima!!
Passo 4
Agora vamos aplicar os mesmos números para o para achar o valor da baçança de baixo!
Podemos substituir aí :