Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 58
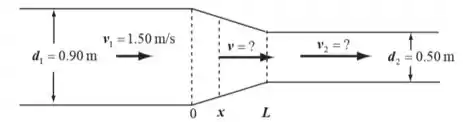
Água escoa através de um cano de 1,0 m de comprimento e de seção cônica, que conecta um cilíndrico de 0,45 m de raio, à esquerda, com um cano cilíndrico de 0,25 m de raio, à direita. Se a água fui dentro do cano de 0,45 m com uma rapidez de 1,50 m/s, (a) qual é a rapidez do fluxo no cano de 0,25 m? (b) Qual é a rapidez do fluxo em uma posição x da seção cônica, se x é a distância medida da extremidade da esquerda desta seção.
Passo 1
Vamos fazer um esqueminha da questão só para facilitar.
Temos a seção 1, antes da parte do cone, e a seção 2, depois da parte do cone. E temos uma seção genérica dentro da parte cônica. Aí reunindo os dados que ele deu sobre essas seções num desenho:
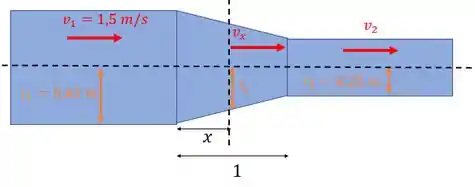
a) Queremos descobrir . Como o fluido que temos é água, podemos considerar que ele é incompressível e que assim vale o principio da continuidade, que diz que a vazão volumétrica é a mesma em todos os pontos.
Assim temos que as vazões volumétricas nos pontos 1 e 2 são iguais.
Onde:
e são as áreas das respectivas seções
e são as velocidades de fluxo nas respectivas seções
Logo, como queremos saber o valor numérico de , vamos isolá-lo na equação, meus queridos:
Como ele nos deu raios das seções, consideramos que as seções são circulares
Como consequência disso:
Agora, vamos aplicar os valores dados pela questão:
Passo 2
b) Queremos a velocidade na parte cônica em função de . Não se assusta com a reposta em função de , calma, a gente vai conseguir.
Para resolvermos a letra b) iremos seguir alguns passos, mas, inicialmente, vamos fazer uma ilustração do problema:
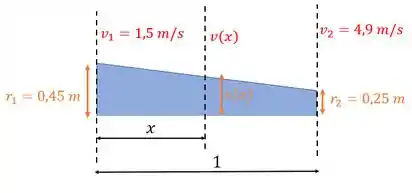
O principio da continuidade vale para todo o tubo, então podemos usa-los novamente. Podemos compara a seção com a seção 1:
Como queremos saber em função apenas da variável vamos isolá-lo:
Lembrando que
Então
Substituindo os dados que temos:
Passo 3
Falta a gente achar o raio em função de , né? Podemos usar semelhança de triângulos, nesse triângulo azul mais escuro
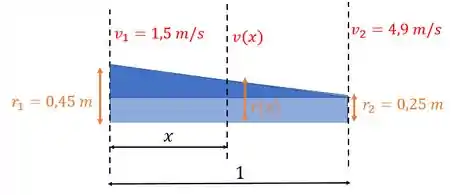
Fazemos assim
Substituindo em :
Resposta
a) b)