Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 55
Responda às questões do Problema 54, mas para uma força que empurra o bloco a um ângulo abaixo da horizontal.
Passo 1
Letra (a):
À medida que a gente aumenta o , a gente dificulta o movimento em duas frentes: primeiro que a componente vertical da F aumenta a força normal, o que só aumenta o atrito. Segundo que a gente diminui a componente horizontal, que é a única coisa que ajuda o bloco andar pra frente.
Passo 2
Letra (b)
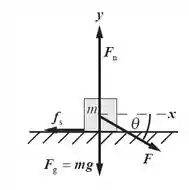
Vamos começar aplicando a segunda lei de Newton:
Só que a gente vai considerar que a força de atrito estático é máxima, ou seja, o bloco está na iminência de se movimentar:
Passo 3
Agora a segunda lei de Newton em y:
Isola a :
Agora joga esse resultado na última equação do passo 2:
Vamos isolar a F:
Passo 4
Vamos jogar os valores:
Vamos calcular o valor de F para vários ângulos. O resultado está aí embaixo:
E um gráfico, em que a gente pode usar um programa de computador, ou alguma ferramenta da internet.
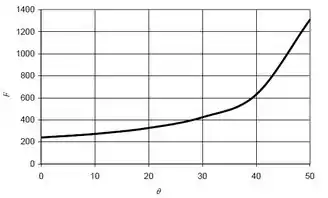
Pelo gráfico, a gente vê que a menor força ocorre para .
Então a gente vai pegar a equação (1) e jogar :
Passo 5
Letra (c)
O ângulo tem que ser 0, porque assim a normal é mínima e a componente horizontal é máxima.
Resposta
Letra (a): Ver solução.
Letra (b):
Letra (c):