Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.Problemas Adicionais - Ex. 98
Considere uma carga pontual e tome V =0 no infinito. (a) Quais são a forma e as dimensões de uma superfície equipotencial com um potencial de 30,0 V produzido exclusivamente pela carga q? (b) As superfícies cujos potenciais diferem de um valor constante (1,0 V, por exemplo) são igualmente espaçadas?
Passo 1
(a) Bem, precisamos descrever uma superfície equipotencial, de potencial , produzida exclusivamente pela carga .
Vamos lembrar que a superfície equipotencial é uma superfície esférica com centro na carga q. Para encontrar o raio dessa esfera, utilizamos:
Colocando o raio, r, em evidência:
Substituindo os valores:
Nossa superfície fica assim:
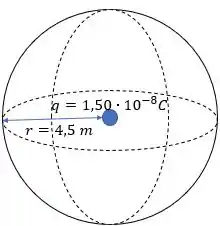
Passo 2
No item (b), devemos ver que o potencial depende de , ou seja, ele é inversamente proporcional ao tamanho do raio. Assim, as superfícies não vão ser igualmente espaçadas, isso só seria verdade se o potencial fosse diretamente proporcional ao raio.
Não sacou? Vamos olhar com mais calma o exemplo acima!
Se o potencial fosse proporcional a , ele seria algo como
Se andássemos uma distância o potencial ficaria
Ou seja, ao passarmos de uma superfície de raio pra outra de raio o potencial aumentou .
Se andarmos agora uma distância
Ou seja, a cada distância que a gente anda o potencial aumenta , o que significa que essas superfícies potenciais que estão distantes umas das outras de têm uma diferença de potencial entre si de , o que é constante!
Beleza, mas o nosso potencial éda seguinte forma
Se andarmos uma distância
A diferença de potencial fica
Aí que dá ruim! Essa diferença de potencial não é mais constante! Ela depende de . Por isso que a distâncias entre superfícies equipotenciais que diferem de um valor constante não equidistantes :D
Feshow?
Resposta
(a)
(b) Não.