Considere os dois vetores e . Calcule
a)
b)
c)
d)
e) as direções de e
Passo 1
Fala ai pessoal tranquilo? Bora matar mais uma questão?
- , possui direção diagonal, eixo positivo e eixo negativo.
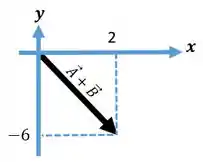
, possui direção diagonal, eixo positivo e eixo positivo.
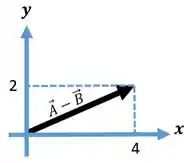
Resposta
- , possui direção diagonal, eixo positivo e eixo negativo.
- , possui direção diagonal, eixo positivo e eixo positivo.