Uma espeleóloga está pesquisando (sugestão: talvez seja mais interessante dizer ‘pesquisadora estudando uma caverna’) uma caverna. Ela percorre em linha reta de leste para oeste, depois caminha em uma direção formando com a direção anterior e em sentido do sul para o leste; a seguir, percorre a no sentido do norte para o oeste. Depois de um quarto deslocamento não medido, ela retorna ao ponto de partida. Use um diagrama em escala para determinar o módulo, a direção e o sentido do quarto deslocamento.

Agora, vamos ver qual foi o trajeto da pesquisadora.

O primeiro deslocamento é de 180m de leste a oeste. Ou seja, olhando na rosa dos ventos vamos ver que ela foi da direita para esquerda. Então, imaginando o ponto inicial da pesquisadora na origem de um plano cartesiano, temos

Como o vetor está totalmente sobre o eixo , ele só terá uma componente que pode ser escrita como:

O plano cartesiano foi desenhado só para entender melhor o sinal negativo, mas será mais fácil representar os vetores sem ele, ok??

O segundo deslocamento, de 210m, faz com o primeiro e vai na direção sul e leste, ou seja, para baixo e para direita (dá uma olhadinha na rosa dos ventos pra não se perder aí).

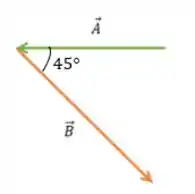
Esse segundo deslocamento não está sobre os eixos, isso significa que ele pode ser decomposto na direção do eixo e na direção do eixo .

Usando a decomposição do vetor para achar suas componentes:

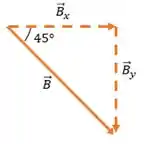
Pra fazer essa decomposição a gente pensa o seguinte. A componente que está colada no ângulo é a que ganha o cosseno, e a componente que está separada do ângulo ganha o seno. (aí você lembra, colada = cosseno, separada = seno)

Juntando as duas para formar o vetor , ficamos com:

Tranquilo até aqui? 😇

O terceiro deslocamento, de 280m, segue na direção norte e oeste, ou seja, pra cima e pra esquerda

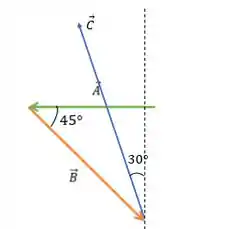
Como esse vetor faz do Norte para o oeste

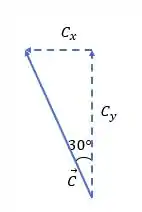
Aqui também vamos decompor esse vetor, já que ele está fora dos eixos. Usando a mesma regra de decomposição que fizemos no , teremos:

O que nos dá:

Bacana, não é? 😊

E agora voltamos de onde partimos!

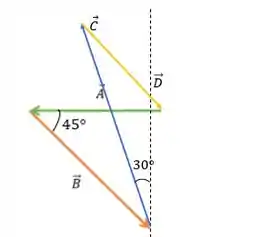
Para achar esse último vetor, que chamaremos de vetor , vamos usar aquela informação que vimos lá no passo , onde a soma de todos os deslocamentos tem que ser o vetor nulo. Assim:

Isolando o vetor , ficamos com:

Agora é só substituir é só substituir todos os vetores que encontramos antes!

agrupando todas as componentes, teremos a representação do vetor . E da forma como está escrito, já carrega as informações de direção e sentido.

Agora só falta achar o módulo.

Para encontrar o módulo de um vetor, nós pegamos as componentes dele e encaixamos nessa formulazinha aqui:

Assim, substituindo na fórmula ficamos com:

E aí! entendeu tudo? Responde Aí! 😁