Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 87
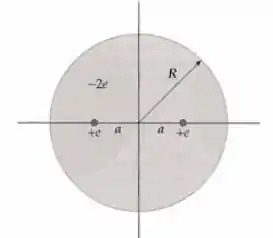
Considere um modelo simples, mas surpreendente preciso para a molécula de hidrogênio: duas cargas puntiformes positivas, cada uma com carga , estão localizadas no interior de uma esfera uniformemente carregada de raio , que tem uma carga igual a . As duas cargas puntiformes estão colocadas simetricamente equidistantes do centro da esfera (Figura 22-48). Determine a distância do centro, , onde a força resultante em cada carga puntiforme é zero.
Passo 1
A força sobre a carga puntiforme será devido a interação com a outra carga e com a esfera. Lembre-se do exercício 83 em que obtivemos que o campo elétrico no interior de uma esfera uniformemente carregada é:
Passo 2
Assim, para que ocorra o equilíbrio, devemos ter
onde
Segue
Resposta
A distância é .
Exercícios de Livros Relacionados
Um quadrado com aresta de 10c m está centrado no eixo x em uma região onde existe um campo elétrico uniforme dado por E → = 2,00k N / Ci ^ . (a) Qual é o fluxo elétrico deste campo elétrico através da
Qual é o fluxo elétrico através de um dos lados de um cubo que tem uma carga puntiforme isolada de - 3,00μ C colocada no seu centro? Dica: você não precisa integrar nenhuma equação para obter a respos
Uma carga puntiforme ( q = + 2,00μ C ) está no centro de uma esfera imaginária que tem raio igual a 0,500m . (a) Determine a área da superfície da esfera. (b) Determine a magnitude do campo elétrico e
Uma carga puntiforme isolada ( q = 2,00μ C ) está fixa na origem. Uma superfície esférica imaginária de raio 3,00m está centrada no eixo x em x = 5,00m . (a) Esboce linhas de campo elétrico para esta
Um campo elétrico é dado por E → = sign x ⋅ 300N / C i ^ , onde sign x é igual a - 1 se x0 , 0 se x = 0 e + 1 se x0 . Um cilindro de comprimento 20c m e raio 4,0c m tem seu centro na origem e seu