Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 8.Problemas - Ex. 40

Considere um sistema de duas partículas no plano x y : m 1   =   2,00   k g está no local   r → 1   =   ( 1,00 i ^   +   2,00 j ^ )   m e tem velocidade de ( 3,00 i ^   +   0,500 j ^ )   m / s ; m 2   =   3,00   k g   está a   r → 2   =   ( – 4,00 i ^   –   3,00 j ^ )   m e tem velocidade   ( 3,00 i ^   –   2,00 j ^ )   m / s . (a) Organize essas partículas em uma grade ou papel de gráfico. Faça o rascunho dos vetores posição e mostre as velocidades. (b) Encontre a posição do centro de massa do sistema e marque-a no diagrama. (c) Determine a velocidade do centro de massa e mostre-a no diagrama. (d) Qual é o momento linear total do sistema?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Ver figura abaixo:

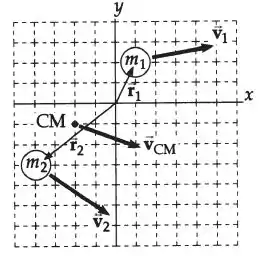
Passo 2

Letra b:

Usando a definição do vetor posição no centro de massa:

r → C M = m 1 r → 1 + m 2 r → 2 m 1 + m 2

r → C M = 1 2.00 k g + 3.00 k g 2.00 k g 1.00 m , 2.00 m + 3.00 k g - 4.00 m , - 3.00 m

r → C M = - 2.00 i ^ - 1.00 j ^ m

Passo 3

Letra c:

A velocidade do centro de massa é:

v → C M = P → M = m 1 v → 1 + m 2 v → 2 m 1 + m 2 = 1 2.00 k g + 3.00 k g [ ( 2.00 k g ) ( 3.00 m / s , 0.50 m / s + ( 3.00 k g ) ( 3.00 m / s , - 2.00 m / s ) ]

Passo 4

Letra d:

O momento linear total do sistema pode ser calculado como:

P → = M v → C M   ou  P → = m 1 v → 1 + m 2 v → 2

Que nos dá:

Resposta

  1. Ver figura
  2. - 2.00 i ^ - 1.00 j ^ m
  3. 3.00 i ^ - 1.00 j ^ m s
  4. 15.0 i ^ - 5.00 j ^ k g ⋅ m s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 9-45 a , um cachorro de 4,5k g está em um barco de 18k g a uma distância D = 6,1m da margem. O animal caminha 2,4m ao longo do barco, na direção da margem, e para. Supondo que não há atrito en
Um automóvel de 1000k g está parado em um sinal de trânsito. No instante em que o sinal abre, o automóvel começa a se mover com uma aceleração constante de 4,0m / s 2 . No mesmo instante um caminhão d
Dois patinadores, um de 65k g e outro de 40k g , estão em uma pista de gelo e seguram as extremidades de uma base de 10m de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste a
Ricardo, com 80k g de massa, e Carmelita, que é mais leve, estão apreciando o pôr-do-sol no lago Mercedes em uma canoa de 30k g . Com a canoa imóvel nas águas calmas do lago, o casal troca de lugar. S
Na Fig. 9-43, duas partículas são lançadas da origm do sistema de coordenadas no instante t = 0 . A partícula 1 , de massa m 1 = 5,00g , é lançada horizontalmente para a direita, em um piso sem atrito