Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.3 - Ex. 17
Na Fig. 9-45, um cachorro de está em um barco de a uma distância da margem. O animal caminha ao longo do barco, na direção da margem, e para. Supondo que não há atrito entre o barco e a água, determine a nova distância entre o cão e a margem. (Sugestão: veja a Fig. 9-45.)
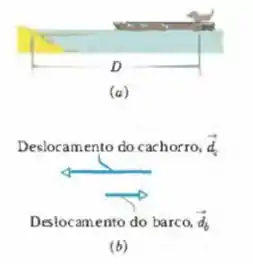
Passo 1
Como a força resultante externa no sistema considerando cachorro-barco é nula, o centro de massa do sistema permanece sempre no mesmo lugar. Portanto, usando a seguinte relação:
E lembrando que o centro de massa não varia a posição:
Isolando :
Passo 2
Agora, fazendo uma análise geométrica, percebemos que o cachorro se deslocou de uma distância em relação ao barco, assim;
Isolando :
Usamos o módulo dos deslocamentos, porque os dois se deslocam em sentidos opostos, porém o centro de massa deve permanecer no mesmo lugar.
Passo 3
Combinando a e a , temos:
Isolando :
Substituindo os valores:
Passo 4
Por fim, sabemos agora que o cachorro está mais próximo da margem em relação a posição inicial . Portanto, a nova distância para margem é: