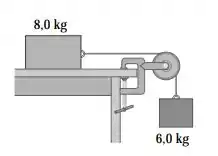
Considere o sistema indicado na Figura 6.37. A corda e a polia possuem massas desprezíveis, e a polia não tem atrito. Inicialmente, o bloco de 6,0 kg desloca-se verticalmente para baixo e o bloco de 8,0 kg desloca-se para a direita, ambos com velocidade de 0,900 m/s. Os blocos entram em repouso após percorrerem 2,0 m. Use o teorema do trabalho-energia para calcular o coeficiente de atrito cinético entre o bloco de 8,0 kg e o topo da mesa.

Agora pensa comigo. Há outra forma de achar o trabalho total, certo? Como? Calculando o trabalho feito por cada forcinha e somando! O trabalho de uma força é dado por

Sendo paralelo a força. Então para ter trabalho a força precisa estar na direção do deslocamento.

Que forças que estão na direção do deslocamento na nossa situação? Primeiro, a força peso do bloco menor. E ela que puxa a galera toda para baixo. Então temos

Como o ela está no mesmo sentido do movimento (o bloquinho está caindo e está para baixo) esse trabalho é positivo. E o enunciado nos diz que a gente anda . Como :

A outra força que está na direção do deslocamento é o atrito. Mas ela está no sentido oposto ao deslocamento, então fica negativo o trabalho, assim:

Esse também é . Temos que essa força é dada por

Só que essa força normal no bloco maior vai ser igual ao peso desse bloco, então:

O trabalho total fica:

Igualando as duas expressões do trabalho total que achamos:

Agora basta substituir os valores e encontrar o valo de :

Prontinho!