Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 8.Problemas Adicionais - Ex. 130

130- Uma mola cuja constante elástica é k = 200   N / m está suspensa verticalmente, com a extremidade superior fixa no teto e a extremidade inferior na posição y = 0. Um bloco de 20 N de peso é preso à extremidade inferior da mola, mantido nessa posição por um momento e depois liberado.

. Determine (a) a energia cinética K,

(b) a variação (a partir do valor inicial) da energia potencial gravitacional ΔUg ,

e (c) a variação da energia potencial elástica ΔUe do sistema bloco-mola quando o bloco está em y = −5,0 cm.

Determine

(d) K,

(e) ΔUg

e (f) ΔUe para y = −10 cm,

(g) K,

(h) ΔUg

e (i) ΔUe para y = −15 cm

e (j) K

, (k) ΔUg

e (l) ΔUe para y = −20 cm

Passo 1

Vamos desenhar o sistema sendo retratado antes de ser solto.

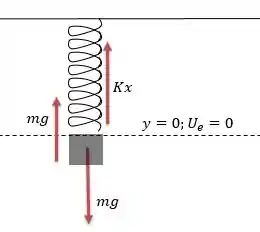
No momento que o bloco é preso temos uma força igual a m g que mantém a mola na posição de equilíbrio da mola. Não tendo nenhuma energia fluindo no sistema.

Agora o bloco é solto, nesse momento o equilíbrio do sistema muda de posição e vai para uma posição onde a força elástica e a força peso são iguais, que é em (dizendo que y é o alongamento da mola):

k y = m g

y = m g k

Logo o sistema fica:

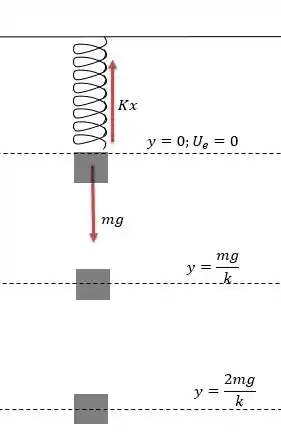
O sistema tenderá a oscilar em torno desse ponto y = m g k esticando e comprimindo essa mola com a mesma amplitude máxima de m g k .

Passo 2

Dados da questão:

k = 200   N / m

m g = 20   N

Com esses valores temos a somatória da energia mecânica do sistema.

E m = K + U e + U g

Onde K é a energia cinética, U e a energia potencial elástica e U g a energia potencial gravitacional. Se o bloco começa relaxado a partir do momento que é solta então pode se dizer que E m = 0 , logo a energia cinética valerá:

K = - U g - U e

E as fórmulas de U g e U e respectivamente serão:

U g = m g y

U e = k x 2 2

Passo 3

Para y = - 0.05   m :

U g = - 20 × 0.05 = - 1   J

U e = 200 2 × - 0.05 2 = 0.25   J

Logo:

K = - - 1 - 0.25 = 0.75   J

Passo 4

Para y = - 0.10   m :

U g = - 20 × 0.1 = - 2   J

U e = 200 2 × - 0.1 2 = 1   J

Logo:

K = - - 2 - 1 = 1   J

Passo 5

Para y = - 0.1 5   m :

U g = - 20 × 0.15 = - 3   J

U e = 200 2 × - 0.1 5 2 = 2 . 25   J

Logo:

K = - - 3 - 2.25 = 0 . 75   J

Passo 6

Para y = - 0.2   m :

U g = - 20 × 0.2 = - 4   J

U e = 200 2 × - 0.2 2 = 4   J

Logo:

K = - - 4 - 4 = 0   J

Resposta

a )   0.75   J           b ) - 1 J       c ) 0.25   J

d )   1   J         e ) - 2   J       f )   1   J

g )   0.75   J     h )   - 3   J     i )     2.25   J

j )   0   J     k ) - 4   J       l ) 4   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Fig. 8-39a se refere à mola de uma espingarda de rolha (Fig. 8-39b); ela mostra a força da mola em função da distensão ou compressão da mola. A mola é comprimida 5,5c m e usada para impulsionar uma
Na Fig. 8-40, um bloco de massa m = 12k g é liberado a partir do repouso em um plano inclinado sem atrito de ângulo θ = 30 ° . Abaixo do bloco há uma mola que pode ser comprimida 2,0c m por uma força
Uma caixa de pão de 2,0k g sobre um plano inclinado sem atrito de ângulo θ = 40,0 ° está presa, por uma corda que passa por uma polia, a uma mola de constante elástica k = 120N / m , como mostra a Fig
Uma mola ( k = 200N / m ) está presa no alto de um plano inclinado sem atrito com θ = 40 ° (Fig. 8-57). Um bloco de 1,0k g é lançado para cima ao longo do plano, de uma posição inicial que está a uma
A Fig. 8-34 mostra uma pedra de 8,00k g em repouso sobre uma mola. A mola é comprimida 10,0c m pela pedra. (a) Qual é a constante elástica da mola? (b) A pedra é empurrada mais 30c m para baixo e libe