Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 67

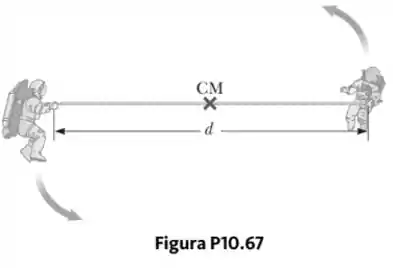
Dois astronautas (Fig. P10.67), cada um com massa de 75,0   k g , estão conectados por uma corda de 10,0   m de massa desprezível. Eles estão isolados no espaço, orbitando seu centro de massa com velocidade 5,00   m / s . Tratando os astronautas como partículas, calcule

  1. o módulo do momento angular do sistema de dois astronautas e
  2. a energia rotacional do sistema.

    3. Ao puxar a corda, um dos astronautas encurta a distância entre eles em 5,00   m .

  3. Qual é o novo momento angular do sistema?
  4. Quais são as novas velocidades dos astronautas?
  5. Qual é a nova energia rotacional do sistema?
  6. Quanta energia potencial química no corpo do astronauta foi convertida em energia mecânica no sistema quando ele encurtou a corda?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

A magnitude do momento angular é | L → | = m | r → × v → | . Neste caso, r e v são perpendiculares, então a magnitude de L sobre o centro de massa é:

L = ∑ m r v = 2 75.0 k g 5.00 m × ( 5.00 m / s )

= 3.75 × 10 3 k g ⋅ m 2 s

Passo 2

Letra b:

K i = 1 2 m 1 v 1 i 2 + 1 2 m 2 v 2 i 2 K i = 2 1 2 ( 75.0 k g ) ( 5.00 m / s ) 2 = 1.88 k J

Passo 3

Letra c:

Com um braço de alavanca de zero, a tensão do cabo não gera torque sobre o centro de massa. Assim, o momento angular para o sistema permanece inalterado:

L f = L i = 3750 k g ⋅ m 2 s

Passo 4

Letra d:

v f = L f 2 m r f = 3750 k g ⋅ m 2 s 2 75.0 k g 2.50 m = 10.0 m s

Passo 5

Letra e:

K f = 2 1 2 ( 75.0 k g ) ( 10.0 m / s ) 2 = 7.50 k J

Passo 6

Letra f:

Se o trabalho realizado pelo astronauta for totalmente possível pela conversão de energia química em energia mecânica, então a energia potencial química necessária é:

W = K f - K i = 5.62 k J

Resposta

  1. 3.75 × 10 3 k g ⋅ m 2 / s
  2. 1.88 k J
  3. 3750 k g ⋅ m 2 s
  4. 10.0 m s
  5. 7.50 k J
  6. 5.62 k J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois discos estão montados (como um carrossel) no mesmo eixo, com rolamentos de baixo atrito, e podem ser acoplados e girar como se fossem um só disco. O primeiro disco, com um momento de inércia de 3
O rotor de um motor elétrico tem um momento de inércia I m = 2.10 - 3 k g m ² ² em relação ao seu eixo central. O motor é usado para mudar a orientação da sonda espacial no qual está montado. O eixo d
Uma roda está girando livremente com uma velocidade angular de 800 r e v / m i n em torno de um eixo cujo momento de inércia é desprezível. Uma segunda roda, inicialmente em repouso e com momento de i
Uma barata de massa m está na borda de um disco homogêneo de massa 4 m que pode girar livremente em torno do centro como um carrossel. Inicialmente, a barata e o disco giram juntos, com uma velocidade
Uma pequena esfera maciça com 0,25 c m de raio e uma massa de 0,56 g rola sem deslizar no interior de um grande hemisfério fixo com 15 c m de raio e um eixo de simetria vertical. A esfera parte do rep