Na figura, um fio de alumínio de comprimento e seção reta e massa específica e mesma seção reta. O fio composto, tensionado por um bloco de massa , está disposto de tal forma que a distância entre o ponto de solda e a polia é . Ondas transversais são excitadas no fio por uma fonte externa de frequência variável; um nó está situado na polia. (a)Determine a menor frequência que produz uma onda estacionária tendo o ponto de solda como um dos nós. (b) Quantos nós são observados para essa freqüência?
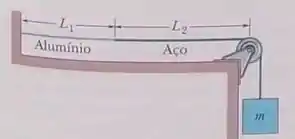
Passo 1
(a)Vamos entender primeiro o que acontece quando o fio é excitado. Como as duas seções dele são excitadas por uma mesma fonte, que transmite sua freqüência da vibração para ambas, elas vibram com uma mesma freqüência.
Beleza! Mas e quanto à velocidade e o comprimento de onda? Eles dependem das propriedades do meio de propagação da onda! Por isso são diferentes para o alumínio e para o aço.
Usando o fato de que as freqüências são as mesmas, a gente tem:
Passo 2
Além disso, em ambas as seções acontece que (pois elas estão fixas em ambas as extremidades devido à presença da solda). Então e .
É muuito importante lembrar sempre, também, que , em que e são a tensão na corda e sua densidade linear. Além disso, a densidade volumétrica é dada por . Disso, a gente pode concluir nesse passo que:
Reforçando que as duas seções da corda possuem a mesma área transversal e estão sujeitas a uma mesma tensão . Das duas expressões acima e do fato de que e , vem:
Passo 3
Top! Lembra que a gente achou no passo 2 que e ? Vamos usar essas duas expressões na última do passo 2:
Agora, bora dividir essas duas expressões (os primeiros membros e os segundos). Com isso, a gente tem isso como resultado:
Isolando :
Passo 4
Beleza! A gente viu que , mas como isso pode nos ajudar a encontrar a menor freqüência que produz uma onda estacionária se propagando no fio (composto de dois materiais diferentes)? Ah, meu caro! A chave para essa resposta está no fato de que uma onda estacionária só será obsrvada quando e forem números inteiros. Na verdade, isso significa que em cada seção do fio ondas estacionárias vibrando nos harmônicos e serão formadas.
Daí, a gente tem que encontrar os menores números inteiros e para os quais . Eles são iguais a e . Ótimo! Com e , a gente encontra substituindo um desses valores em ou . Fazendo isso para a primeira, encontramos:
Passo 5
(b)O número total de nós é dado por .
Resposta
(a)
(b) nós