Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 71
Um bloco de madeira leve está sobre um dos pratos de uma balança de braços iguais, onde mantém-se perfeitamente equilibrado pela massa de 0,0950 kg de um bloco de latão colocado no outro prato da balança. Calcule a massa do bloco de madeira leve se a sua densidade for igual a 150 . Explique porque podemos desprezar o empuxo sobre o bloco de latão, mas não o empuxo do ar sobre o bloco de madeira leve.
Passo 1
E ai galera, aqui vamos aplicar a segunda condição de equilíbrio no braço de equilíbrio e aplicar a primeira condição de equilíbrio ao bloco e à massa de latão. A força de flutuação na madeira é dada pelo princípio de Arquimedes e pela força de flutuabilidade na massa de latão é ignorada.
Vamos esboçar os objetos e as forças pra facilitar a visualização;
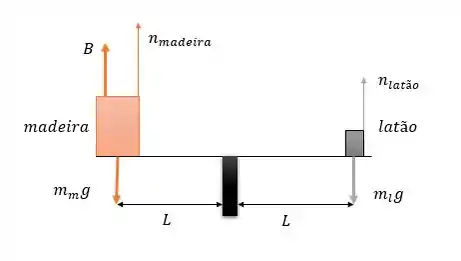
A força flutuante no latão é negligenciada, mas incluímos a força flutuante B no Bloco de madeira, e são forças normais exercidas pelo braço de equilíbrio no qual os objetos estão sentados.
Passo 2
No braço de equilíbrio, temos que
Isso implica que
Passo 3
Vamos, primeiro, esboçar um diagrama de corpo livre para a massa do latão:
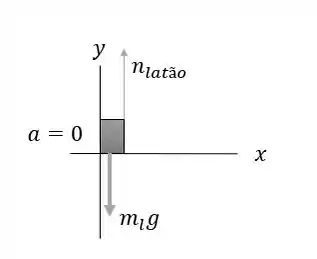
E então, aplicando
Isso implica que
Então,
Passo 4
E então, vamos esboçar o diagrama de corpo livre para o bloco de madeira:
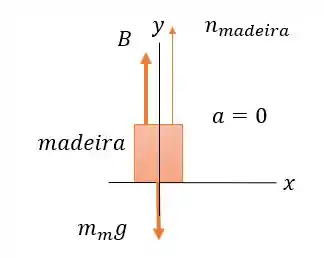
Aplicando
Isso implica que
Passo 5
Mas
Isso implica que
E
Então
Isso implica que
A massa da madeira é maior que a massa do latão; a madeira é parcialmente suportada pela
força de flutuação exercida pelo ar. A flutuabilidade no ar do latão pode ser negligenciada porque a densidade do latão é muito mais que a densidade do ar; a força de flutuação exercida sobre o latão pelo ar é muito menor que o peso do bronze. A densidade da madeira balsa é muito menor que a densidade do latão, de modo que a força de flutuabilidade na madeira de balsa não é uma fração tão pequena do seu peso.