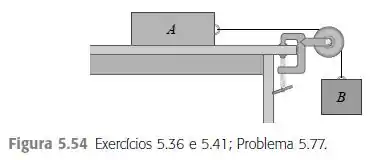
Considere o sistema indicado na Figura . O bloco pesa e o bloco , . Suponha que o bloco desça com velocidade constante. a) Ache o coeficiente de atrito cinético entre o bloco e o topo da mesa. b) Suponha que um gato, também com peso , caia no sono sobre o bloco . Se o bloco agora se move livremente, qual é sua aceleração (módulo, direção e sentido)?

Vamos começar esboçando o diagrama de corpo livre dos blocos:

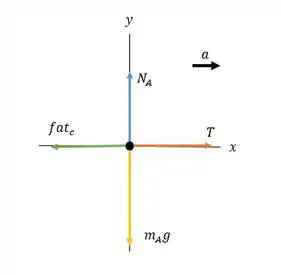
Repare que é a tensão em cada cabo, é a força de atrito cinético, é a força normal de superfície sobre o bloco e e são os pesos de cada bloco.

Assim, considerando o peso , temos que massa dos blocos é dada pela expressão:

Então, temos que a massa do bloco é:

Substituindo os valores que o enunciado nos deu:

E para a massa do bloco , vamos ter:

Então, vamos aplicar as segunda lei de Newton para o bloco B, no caso desse bloco, temos forças agindo apenas no e e uma aceleração, , igual a zero, portanto:

Agora vamos aplicar a segunda lei de Newton para o bloco : (como os dois blocos estão conectados por um fio e a aceleração, , do bloco é igual a zero, consequentemente a aceleração, , do bloco também é igual a zero)

No :

Isolando a tensão :

Como a força nesse cabo é igual ao peso do bloco , substituindo, vamos ter:

No :

Sabemos que a força de atrito se dá pelo coeficiente de atrito vezes a normal, , então:

b) Agora vamos considerar o bloco mais o gato, então vamos ter uma nova massa de :

Como o gato tem o mesmo peso do bloco , que já calculamos, temos que:

Agora, considerando o gato, já temos todas as informações para calcular a força de atrito entre o e a superfície:

A aceleração do bloco tem que ser igual a aceleração do bloco , pois estão conectador por uma corda. Então vamos adicionar as duas equações que encontramos e ficamos com:

Isolando na equação:

E substituindo os valores, temos:

Logo, a aceleração é para cima e o bloco desacelera.

Valeu, galera! Até a próxima! 😉