Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 21
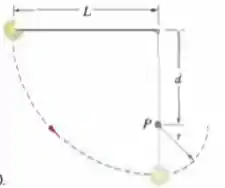
A corda da Fig. 8-36, de comprimento , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância da extremidade fixa a um pino no ponto é . A bola, inicialmente em repouso, é liberada com o fio na posição horizontal, como mostra a figura, e percorre a trajetória indicada pelo arco tracejado. Qual é a velocidade da bola ao atingir (a) o ponto mais baixo da trajetória e (b) o ponto mais alto depois que a corda encosta no pino?
Passo 1
Primeiro, devemos perceber que somente a força gravitacional realiza trabalho durante este deslocamento, tendo em vista que a força de tração está perpendicular ao movimento em todo o instante. Assim, como a força gravitacional é uma força conservativa, podemos afirmar que há conservação da energia mecânica, então:
Inicialmente, como a bola é solta do repouso e considerando o ponto mais baixo como , então há somente energia potencial gravitacional associado a esta bola, no ponto mais baixo , a energia potencial gravitacional se transforma toda em energia cinética. Assim:
Substituindo os valores:
Passo 2
Após atingir o pino, devemos perceber que o a altura máxima que a bola irá atingir é:
Assim, fazendo de maneira análoga ao que fizemos no passo anterior, porém aplicando a conservação da energia mecânica do ponto inicial até este ponto de altura máxima após atingir o pino, temos:
Isolando :
Substituindo os valores:
Resposta
- ;
- .