Tarzan, que pesa 688N , salta de um penhasco pendurado na extremidade de um cipó com 18m de comprimento (Fig. 8-38). Do alto do penhasco até o ponto mais baixo da trajetória, ele desce 3,2m . O cipó se romperá se a força exercida sobre ele exceder 950N . (a) O cipó se rompe? Se a resposta for negativa, qual é a maior força a que é submetido o cipó? Se a resposta for afirmativa, qual é o ângulo que o cipó está fazendo com a vertical no momento em que se rompe?Figura 8-38 - Problema 27

Como o cipó suporta uma Força de 950N , ele não se rompe e a Força máxima a que o cipó está submetido é de 9,3.1 0 2N .

Enunciado

Oi, pessoal! Tudo bom? Vamos começar entendendo as forças que estão atuando na questão!

Inicialmente, toma-se o ponto mais baixo da trajetória como referência. Neste ponto, tem-se a seguinte configuração

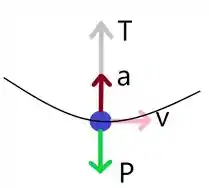
Para o cipó se romper, temos que a força Peso deve ser superior a força de tração. Logo, o cipó não se rompe.

Pela segunda Lei de Newton

Onde é a tração a que está submetida o cipó, é a força peso do Tarzan, é a massa do Tarzan e é a aceleração centrípeta.

Como,

E a aceleração centrípeta é dada por,

sendo a velocidade do Tarzan e o raio (dado pelo comprimento do cipó).

Temos que,

Além disso, neste ponto, toda a energia potencial gravitacional () é transformada em energia cinética (), logo

Colocando em evidência

Combinando as equações encontradas ()

Substituindo os dados fornecidos no problema:

Ficamos com,

Como o cipó suporta uma Força de , ele não se rompe e a Força máxima a que o cipó está submetido é de .