Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 26
Um pêndulo é formado por uma pedra de oscilando na extremidade de uma corda de de comprimento e massa desprezível. A pedra tem uma velocidade de ao passar pelo ponto mais baixo da trajetória. (a) Qual é a velocidade da pedra quando a corda forma um ângulo de com a vertical? (b) Qual é o maior ângulo com a vertical que a corda assume durante o movimento da pedra? (c) Se a energia potencial do sistema pêndulo-Terra é tomada sendo nula na posição mais baixa da pedra, qual é a energia mecânica total do sistema?
Passo 1
(a) Devemos perceber que no pêndulo a única força que realiza trabalho é a força gravitacional, tendo em vista que a força de tração da corda atua na pedra perpendicular ao deslocamento em todos os momentos. Mas sobre o pêndulo como um todo (pedra + corda), apenas a força peso age:
Como a força gravitacional é uma força conservativa, então podemos afirmar que há conservação da energia mecânica durante o movimento da pedra. Assim, aplicando a conservação de energia do ponto em que a pedra está passando no ponto mais baixo (, que é a imagem acima) e o ponto que o pêndulo faz um ângulo de com a vertical:
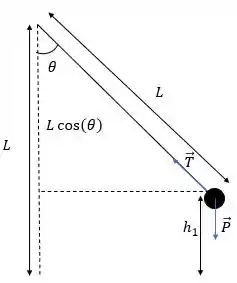
Onde é o comprimento da corda.
Dessa forma, comparando as duas imagens, podemos ver que antes a pedra tinha apenas energia cinética, já que estava na altura e depois passa a ter tanto energia cinética quanto potencial gravitacional, estando a uma altura . Logo, pela conservação de energia:
Como queremos a velocidade final, vamos isolar o :
Podemos dividir toda a equação por e multiplicar por :
Dessa forma:
Pela segunda imagem, podemos ver que , então:
Substituindo os valores:
Passo 2
(c) Bom, o pensamento é o mesmo da letra anterior, a diferença é que, agora, queremos o ponto máximo que a pedra atinge. Na altura máxima, a pedra tem , pois ela estava subindo e está prestes a descer. Então, agora, ela tinha energia cinética e transformou toda essa energia em potencial gravitacional!
Como falado anteriormente, a energia mecânica do sistema se conserva, portanto, aplicando a conservação da energia mecânica no ponto mais baixo e no ponto de retorno:
Lembrando que , porém, neste caso, não conhecemos o :
Simplificando :
Colocando em evidência:
Isolando :
Isolando o :
Substituindo os valores:
Passo 3
(c) Cara, vimos o tempo todo que a energia mecânica se conserva, então podemos pegar qualquer ponto da trajetória para calcular a energia mecânica! Vamos pegar o ponto mais baixo, pois é o mais tranquilo também, só tendo energia cinética nele.
Para calcular a energia mecânica total do sistema:
Resposta
- ;
- ;
- .