Para formar um pêndulo, uma bola de é presa em uma das extremidades de uma haste de de comprimento e massa desprezível; a outra extremidade da haste é montada em um eixo. A haste é levantada até a bola ficar verticalmente acima do eixo e liberada a partir do repouso. Quando a bola atinge o ponto mais baixo, quais são (a) a velocidade da bola e (b) a tensão da haste? Em seguida, a haste é colocada na horizontal e liberada a partir do repouso. (c) Para que ângulo em relação à vertical a tensão da haste é igual ao peso da bola? (d) Se a massa da bola aumenta, a resposta do item (c) aumenta, diminui ou permanece a mesma?
Passo 1
a) No primeiro instante, temos a seguinte configuração
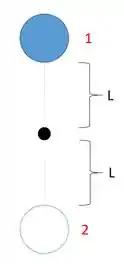
Em , (bola em repouso) e tomando como referência da energia potencial gravitacional.
Em , e , logo, pela lei da conservação de energia
Para e
Passo 2
b) No ponto mais baixo temos o diagrama de corpo livre mostrado na figura abaixo
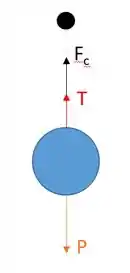
A força centrípeta será
E sabendo que a resultante das forças atuantes no corpo () será igual a força centrípeta, temos
Para
Passo 3
c) No 2° momento teremos a seguinte configuração
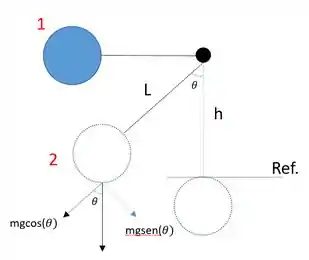
Para o instante temos
Como queremos
Aplicando a lei da conservação de energia nos pontos e
Com
Passo 4
d) Ao calcular o item anterior, nota-se que não há uma dependência com a massa, logo o ângulo permanece o mesmo.
Resposta
a)
b)
c)
d) permanece o mesmo.