Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.5 - Ex. 17

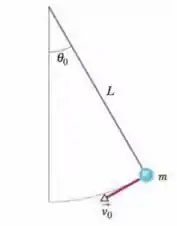
A Fig. 8-32 mostra um pêndulo de comprimento L = 1,25   m . O peso do pêndulo (no qual está concentrada, para efeitos práticos, toda a massa) tem velocidade v 0 quando a corda faz um ângulo θ 0 = 40,0 ° com a vertical. (a) Qual é a velocidade do peso quando está na posição mais baixa se v 0 = 8,00   m / s ? Qual é o menor valor de v 0 para o qual o pêndulo oscila para baixo e depois para cima (b) até a posição horizontal e (c) até a posição vertical com a corda esticada? (d) As respostas dos itens (b) e (c) aumentam, diminuem ou permanecem as mesmas de θ 0 aumentar de alguns graus?

Passo 1

Lembrando que podemos calculcar a altura inicial em relação ao ponto mais baixo alcançado pela bola pela seguinte relação:

h 0 = L 1 - cos ⁡ θ 0

Lembrando que somente o peso realiza trabalho no movimento do pêndulo, pois a tensão da corda atua perpendicular ao deslocamente, então podemos aplicar a conservação da energia mecânica. Então, aplicando a conservação do ponto inicial dado até o ponto mais baixo da trajetória:

m v 0 2 2 + m g h 0 = m v b 2 2

Isolando v b :

v b = v 0 2 + 2 g L 1 - cos ⁡ θ 0

Substituindo os valores:

v b = 8 2 + 2 × 9,8 × 1,25 × 1 - cos ⁡ 40 ° = 8,35   m / s

Passo 2

Aqui queremos encontrar a velocidade inicial para o qual o peso chega à posição horizontal com velocidade nula. Assim, devemos perceber que v f = 0 e θ f = 90 ° . Portanto, aplicando a conservação da energia mecância entre o ponto inicial e a posição horizontal:

m v 0 ' 2 2 + m g h 0 = m g L

Assim, isolando v 0 ' :

v 0 ' = 2 g L - h 0

v 0 ' = 2 g L - L 1 - cos ⁡ θ 0 = 2 g L cos ⁡ θ 0

Substituindo os valores:

v 0 ' = 2 × 9,8 × 1,25 × cos ⁡ 40 ° = 4,33   m / s

Passo 3

Neste caso, faremos a suposição que a tração tende a zero, assim, pela seguna lei de Newton a resultante centrípeta será apenas a força peso no ponto mais alto:

m g = m a c

m g = m v 2 L

Assim, isolando v 2 :

v 2 = g L

Com a velocidade que deve chegar no ponto mais alto em mãos, podemos aplicar a conservação da energia mecânica do ponto inicial até o ponto mais alto:

m v 0 ' ' 2 2 + m g h 0 = m v 2 2 + m g 2 L

Isolando v 0 ' ' :

v 0 ' ' = v 2 + 2 g 2 L - h 0

v 0 ' ' = g L + 2 g 2 L - L 1 - cos ⁡ θ 0

v 0 ' ' = g L + 2 g L 1 + cos ⁡ θ 0

Substituindo os valores conhecidos:

v 0 ' ' = 9,8 × 1,25 + 2 × 9,8 × 1,25 1 + cos ⁡ 40 ° = 7,45   m / s

Passo 4

Quanto maior a energia potencial gravitacional inicial, a bolinha demandará menos energia cinética para alcançar os pontos pedidos nos itens b e c . Portanto, aumentar o θ 0 significa aumenta a energia potencial gravitacional inicial, assim, um valor maior de θ 0 corresponderá em valores MENORES de v 0 ' e v 0 ' ' .

Resposta

  1. v b = 8,35   m / s ;
  2. v 0 ' = 4,33   m / s ;
  3. v 0 ' ' = 7,45   m / s ;
  4. M e n o r e s .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Tarzan, que pesa 688N , salta de um penhasco pendurado na extremidade de um cipó com 18m de comprimento (Fig. 8-38). Do alto do penhasco até o ponto mais baixo da trajetória, ele desce 3,2m . O cipó s
Para formar um pêndulo, uma bola de 0,092k g é presa em uma das extremidades de uma haste de 0,62m de comprimento e massa desprezível; a outra extremidade da haste é montada em um eixo. A haste é leva
A corda da Fig. 8-36, de comprimento L = 120c m , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância d da extremidade fixa a um pino no ponto P é 75,0c m . A b
Um pêndulo é formado por uma pedra de 2,0k g oscilando na extremidade de uma corda de 4,0m de comprimento e massa desprezível. A pedra tem uma velocidade de 8,0m / s ao passar pelo ponto mais baixo da
126- Para fazer um pêndulo, uma bola de 300 g é presa a uma das extremidades de uma corda com 1,4 m de comprimento e massa desprezível. (A outra extremidade da corda está fixa.) A bola é puxada para u