Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 97

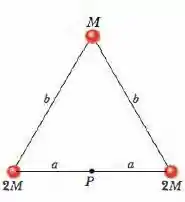
O corpo rígido mostrado na Fig. 10-54 é formado por três partículas ligadas por barras de massa desprezível. O corpo gira em torno de um eixo perpendicular ao plano das três partículas que passa pelo ponto P . Se M   =   0,40   k g , a   =   30   c m e b   =   50   c m , qual é o trabalho necessário para levar o corpo do repouso até a velocidade angular de 5,0   r a d / s ?

Passo 1

Belezera galerinha, quando o enunciado diz que precisa levar o corpo a velocidade angular de 5,0   rad/s , ele está nos dizendo que quer iniciar um movimento circular com o corpo, no caso em torno de um ponto situado em P :

O trabalho que devemos exercer pra colocar um corpo de momento de inércia I em movimento circular com velocidade ω é dado pela fórmula:

W = 1 2 I ω 2

Então como já sabemos a velocidade angular ω = 5,0   rad/s , precisamos encontrar somente o momento de inércia I do sistema de partículas em relação ao ponto P . Então bora lá fazer isso!!

Passo 2

O momento de inércia é calculado pelo produto das massas pelo quadrado das distâncias, dado pela expressão:

I = ∑ i = 1 n m i r i 2

No nosso sistema, temos 3 particulas. As duas que possuem massa 2 M estão sob o mesmo segmento que corta o ponto P , e já nos foi dado então que as distância que elas possuem do ponto P são:

r 1 = a ,     r 2 = a

Agora a terceira partícula, de massa M , está a uma distância perpendicular r 3 dada de acordo com a figura:

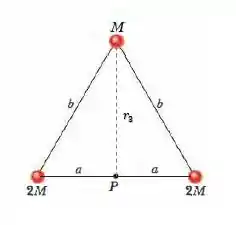
Onde aplicando teorema de Pitágoras, descobrimos que:

r 3 = b 2 - a 2

Passo 3

Iradoso, então se a gente usar a fórmula do momento de inércia, verificamos que:

I = ∑ i = 1 n m i r i 2

I = 2 M a 2 + 2 M a 2 + M b 2 - a 2

Logo:

I = 3 a 2 + b 2 M

E se a gente aplicar na fórmula do trabalhos, obtemos que:

W = 1 2 I ω 2

W = 1 2 3 a 2 + b 2 M ω 2

Então para M = 0,40   kg , ω = 5,0   rad/s ,   a = 0,30   m   e b = 0,50   m . Obtemos que:

W = 1 2 0,208   kg. m 2 5,0   rad/s 2

W = 2,6   J

Resposta

W = 2,6   J

Tranquilo galera? Bora resolver mais questões então

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um volante de motor a gasolina deve fornecer uma energia cinética igual a 500J , quando sua velocidade angular diminui de 650r e v / m i n para 520r e v / m i n . Qual é o momento de inércia necessári
Suponha que o cilindro maciço do dispositivo descrito no Exemplo 9.9 (Seção 9.4) seja substituído por uma casca cilíndrica com o mesmo raioR e com a mesma massa M . O cilindro é ligado ao eixo por mei
Você deve projetar uma plataforma giratória industrial com 60,0c m de diâmetro e energia cinética de 0,250J quando gira a 45,0r p m( r e v / m i n ) . a) Qual deve ser o momento de inércia da platafor
Uma corda leve e flexível é enrolada diversas vezes em torno da periferia de uma casca cilíndrica com raio de 0,25m e massa igual a 40,0N , que gira sem atrito em torno de um eixo horizontal fixo. O c
Energia da Lua? Suponha que em algum momento no futuro você decida explorar a energia rotacional da Lua para uso na Terra. Além dos dados de astronomia no Apêndice F, você pode necessitar saber que a