Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 71
Uma força atuando sobre uma partícula do plano xy, nas coordenadas (x, y), é dada por onde é uma constante positiva e r é a distância dapartícula à origem. (a) Mostre que a magnitude desta força é e que sua orientação é perpendicular a . (b) Encontre o trabalho realizado pela força sobre a partícula, quando esta completa uma volta em um círculo de 5,0 m de raio centrado na origem.
Passo 1
Letra (a)
Temos um errinho de tradução ali no enunciado tá? O deve estar no denominador e não multiplicado por . Agora vamos começar!
Nosso vetor é:
A componente dele é o termo multiplicado por :
E a componente é o termo multiplicado por :
Para achar a magnitude do vetor força como ele pede, a gente tira o módulo do vetor:
Substituindo e :
Passo 2
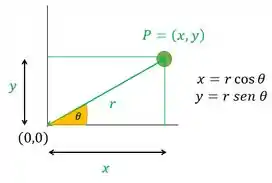
Só que é a distância de um ponto qualquer até a origem. Olha nessa figura:
Usando Pitagoras, podemos escrever essa distância como . Substituindo isso no módulo de :
Passo 3
Para mostrar que dois vetores são perpendiculares o que a gente pode fazer? Cara, a gente pode provar que o produto escalar entre eles é nulo!
Então para mostrar que a força é perpendicular à direção a gente faz o produto escalar entre eles
A gente pode deixar em evidência mesmo. Aí faz o produto entre os coeficientes de e soma ao produto dos coeficientes de :
Conseguimos!
Passo 4
Letra (b)
Para saber o trabalho, a gente tem que saber se o sentido é horário ou anti-horário. Um resultado vai ser o outro multiplicado por -1. Vamos fazer no sentido anti-horário primeiro.
Como a força depende de e , a gente vai usar o formato de integral para calcular o trabalho:
Mas antes de substituir, como o caminho da partícula é circular, a gente vai descrever ele usando coordenadas polares, colocando e em função do raio do círculo (que é a distância de todos os pontos dele a origem e vale ) e :
Substituindo e na força:
Passo 5
Aquele é o vetor posição de um ponto que pertence ao círculo. A gente vai escrever esse vetor posição assim:
Que é o mesmo que
Substituindo as coordenadas polares nele também:
Mas a integral usa , então a gente precisa derivar esse carinha em relação a , derivando cada componente dele, assim:
Isolando quem a gente quer:
Passo 6
Vamos montar a integral. Tínhamos:
Substituindo o que a gente achou e calculando esse produto escalar:
Percebe que é o raio do círculo, então ele é constante. Podemos tirá-lo da integral. E percebe que nossa variável da integral é . Como temos o círculo completo, nosso ângulo dá a volta completa, ou seja,
A integral fica:
Aquele termo em parênteses é parte da identidade trigonométrica , assim:
Passo 7
Substituindo o valor de :
Se fosse no sentido horário:
Resposta
Letra (a): ver solução
Letra (b): ou