Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 110

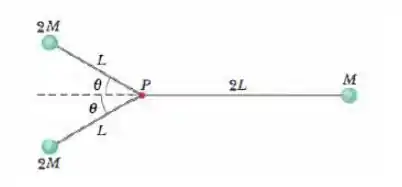
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezível. Determine a energia cinética de rotação do corpo se a velocidade angular é 1,2 r a d / s em relação

( a ) a um eixo que passa pelo ponto P e é perpendicular ao plano do papel;

( b ) a um eixo que passa pelo ponto P , é perpendicular à barra de comprimento 2 L e está no plano do papel.

Passo 1

Olá pessoal, tudo bem? Vamos praticar o cálculo de momento de inércia?

Como o eixo de rotação é perpendicular ao plano da página e as barras tem massa desprezível, podemos aplicar direto a fórmula para o momento de inércia:

I = m r 2 = 2 M L 2 + 2 M L 2 + M 2 L 2 = 8 M L 2

I = 8.1,6 . 0,6 2 = 4,61 k g . m ²

Assim a energia cinética é:

E = I ω 2 2 = 4,61 . 1,2 2 2 = 3,31 J

Passo 2

Agora o eixo de rotação segue sendo perpendicular à barra, mas é no plano do papel. Dá uma espiada no desenho:

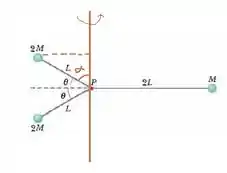
Para calcular o momento de inércia referente a esse novo eixo é preciso conhecer a distância perpendicular das massas ao eixio. Bom, da massa M é tranquilo de ver que a distância é 2 L . Agora o pulo do gato é ver a distância das massas 2 M . Elas fazem um ângulo de 30 ° com o eixo horizontal, sendo assim a distância d vai ser relacionado com o c o s 30 ou com o s e n α , e podemos ver que α = 90 - 30 = 60 ! Então aqui muito cuidado! Para usar a função s e n o temos que achar o ângulo entre a distância até a massa e a linha ao longo do eixo de rotação!

Sendo assim, podemos substituir na fórmula do cálculo do momento de inércia:

I = m r 2 = 2 M [ L . s e n ( 60 ° ) ] 2 + 2 M [ L . s e n ( 60 ° ) ] 2 + M 2 L 2 = 4 M L 3 2 2 + 4 M L 2

I = 3 M L 2 + 4 M L ² = 7 M L ² = 7.1,6 . 0,6 2 = 4,03 k g . m ²

Aí é só calcular a energia cinética:

E = I ω 2 2 = 4,03 . 1,2 2 2 = 2,9 J

É isso! Vamos pra próxima?

Resposta

a 3,31 J  

b 2,90 J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exatamente uma volta de uma corda flexível de massa m é enrolada na periferia de um cilindro uniforme maciço de massa M e raio R. O cilindro gira sem atrito em torno de um eixo horizontal ao longo do
Uma placa de sinalização em metal de uma concessionária de automóveis é um triângulo retângulo delgado com base de comprimento b e altura h. A placa possui massa M. a) Qualé o momento de inércia da pl
Uma régua de um metro e massa igual a 0,160 kg possui um pivô em uma de suas extremidades de modo que ela pode girar sem atrito em torno de um eixo horizontal. A régua é mantida em uma posição horizon
No sistema indicado na Figura 9.18, uma massa de 12,0 kg é libertada do repouso e cai, fazendo com que o cilindro uniforme de 10,0 kg e diâmetro de 30,0 cm gire em torno de um eixo sem atrito que pass
Um ônibus de passageiro em Zurique, na Suíça, usa sua potência motora oriunda da energia acumulada em um volante grande. Utilizando-se de energia da rede elétrica, a roda é colocadaem movimento period