Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.Problemas - Ex. 81

Uma placa de sinalização em metal de uma concessionária de automóveis é um tri��ngulo retângulo delgado com base de comprimento b e altura h. A placa possui massa M. a) Qual

é o momento de inércia da placa para uma rotação em torno do lado de comprimento h? b) Se M = 5,40   k g , b = 1,60   m   e h = 1,20   m , qual é a energia cinética da placa quando ela gira em torno de um eixo com 1,20 m de lado a 2,0   r e v / s ?

Passo 1

Oi, galerinha! Tudo bom?

Vamos começar esboçando a situação para entender melhor! Isso nos dá que:

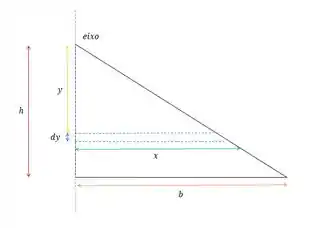
Assim, considerando uma pequena faixa de largura d y   e uma distância y abaixo do topo do triângulo.

O comprimento da tira será:

x = y h b

Como temos uma variação no eixo de rotação, encontraremos o momento de inércia a partir de:

I = ∫ r 2 d m

Agora precisamos achar quem é d m antes de integrar!

Veja só!

Passo 2

A faixa tem área

x   d y

E a área do sinal é

1 2 b h

então a massa da tira é dada por:

d m = M x   d y   1 2 b h = M y b h 2   d y b h

d m = 2 M h 2 y d y

E então,

d I = 1 3 d m x 2 = 2 M b 2 3 h 2 y 3   d y

Isso implica que:

I = ∫ 0 h d I = 2 M b 2 3 h 2 ∫ 0 h y 3 d y = 2 M b 2 3 h 4 1 4 y 4 h 0

I = 1 6 M b 2

Tranquilo até aqui?

Passo 3

Temos que:

I = 1 6 M b 2

Substituindos os valores,

I = 1 6 5,40   k g ⋅ 1,60   m 2 = 2,304 k g ⋅ m 2  

E

ω = 2 r e v s = 4 π r a d s

A energia cinética é dada por:

K = 1 2 I ω 2

Substituindos os valores,

K = 1 2 ⋅ 2,304 k g ⋅ m 2 ⋅ 4 π r a d s 2

K = 182 J

E aí! O que achou? Responde Aí!

Resposta

  1. I = 1 6 M b 2
  2. K = 182 J
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera maciça, de 1,4 k g e 15 c m de diâmetro, está girando em torno de seu diâmetro a 70r e v / m i n . (a) Qual é sua energia cinética? (b) Adicionando-se 5,0 m J de energia à energia cinética,
Um disco uniforme, de massa M e raio R , pode girar livremente em torno de um eixo fixo horizontal que passa pelo seu centro de massa perpendicularmente ao seu plano. Uma pequena partícula de massa m
Um anel uniforme de 1,5 m de diâmetro pivota em torno de um ponto de seu perímetro, livre para girar em torno de um eixo horizontal perpendicular ao seu plano. O anel é largado com seu centro à mesma
Você está projetando um carro que utiliza a energia armazenada em um volante que consiste em um cilindro uniforme de 100k g , de raio R , e que tem uma rapidez angular máxima de 400r e v / s . O volan
Em fevereiro de 2002, um total de 60,7 bilhöes de kWh de energia elétrica foi gerado por usinas nucleares nos Estados Unidos. Nesta época, a população dos Estados Unidos era de cerca de 287 milhöes de