Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 99
Um corredor, viajando com a rapidez constante de 125 km/h, passa por um cartaz. Um carro-patrula parte do repouso, com aceleração constante de (80 km/h)/s até atingir sua rapidez máxima de 190 km/h, que é mantida até alcançar o corredor. (a) Quanto tempo leva o carro-patrulha para alcançar o corredor se ele arranca exatamente quando o corredor passa? (b) Qual a distância percorrida por cada carro? (c) Esboce x(t) para cada carro.
Passo 1
(a) Olá, querido! Vamos lá!
Então, temos um corredor e um policial. Como o policial arranca quando o corredor passa por ele, mas entender como a origem do nosso referencial esse ponto de onde o policial arranca.
O que ele quer saber é quando, depois desse arranque, o policial alcança o corredor.
Primeiro vamos converter nossas unidades. Tudo que está tem em vamos converter para . Para fazer essa conversão, dividimos o valor que temos por 3,6:
Nós sabemos que o policial alcançará o corredor quando suas posições finais forem iguais.
Então a ideia é escrever a equação da posição para cada um deles e igualar para achar (o tempo que leva para eles estarem na mesma posição). Vamos!
Passo 2
O movimento do policial tem duas partes. O enunciado diz que primeiro ele arranca com aceleração constante até atingir
E depois disso sua velocidade fica constante, e só depois disso ele alcança o corredor. Então a gente precisa escrever uma equação que represente esses dois momentos.
Vamos descobrir primeiro o quanto ele alcança enquanto acelera e quanto tempo leva nesse trajeto. Podemos usar a expressão da definição de aceleração:
Ele saiu inicialmente do repouso, , , até , com uma aceleração de . Substituindo e isolando :
Com o tempo de aceleração, podemos encontrar a distância de aceleração usando essa expressão da aceleração constante:
Como o policial parte do repouso, :
Passo 3
Agora pensa comigo: ele andou e depois ficou um tempo com velocidade constante. Então a função posição dele vai ser mais a distância que ele pode andar com velocidade constante depois do tempo .
A gente pode usar a equação da velocidade média aqui para escrever essa distância:
Já vimos que ele andou no tempo . E que depois ele vai ter a velocidade média (constante) de , então vamos substituir isso
Isolando , e chamando de (posição do policial), vamos ficar com:
Já o movimento do corredor é dado pela equação horária da posição quando a gente tem velocidade constante de e começa de :
A gente chamou o de só para ficar com a mesma variável da equação do policial, ok? Como a posição final do corredor e do policial devem ser iguais, fazemos: :
Isolando :
Esse é o tempo que o policial leva para alcançar o corredor.
Passo 4
(b)Para descobrir a distância total, é só substituir o tempo que a gente achou em uma das equações (já que a posição final deles é a mesma, eles vão ter percorrido a mesma distância total).
Vamos usar a equação do policial:
E vai ser igual para os dois, já que ambos partiram do mesmo lugar e também foram até o mesmo lugar.
Passo 5
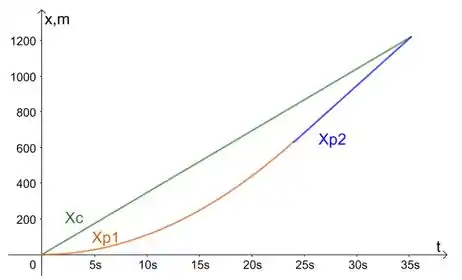
(c)O gráfico da posição como função do tempo para o corredor é apenas uma reta, já que ele tem velocidade constante, e é dado pela equação posição que a gente achou para ele:
Já o gráfico do policial vai ter duas partes. Primeiro a parte entre e , onde ele anda com aceleração constante. Essa vai ser dada pela equação horária da posição quando temos aceleração constante e saímos de e do repouso :
E a segunda parte é a parte onde temos velocidade constante, a partir de . Usamos a equação do passo 3:
Plotando essas 3 curvas, vamos ter esse gráfico:
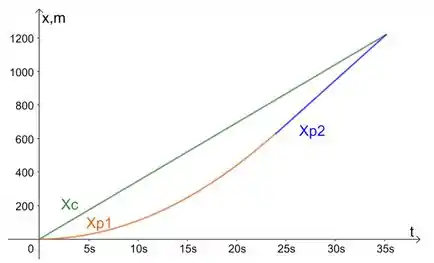
Resposta
c)
