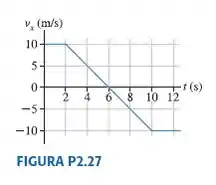
A FIGURA P2.27 mostra o gráfico da velocidade de uma partícula cuja posição inicial é em .
a. Em que instante ou instantes a partícula se encontra em ? Trabalhe com a geometria do gráfico, e não com as equações cinemáticas.
b. Desenhe um diagrama de movimento para a partícula.
Passo 1
Galera, vamos nos referir ao gráfico do enunciado (Figura P2.27).
- Podemos calcular a posição da partícula a cada instante com a equação:
- A partícula se move para a direita por , onde a velocidade é positiva. Atinge um ponto de viragem em em . O movimento é para a esquerda por . Isso é mostrado no diagrama de movimento abaixo.
A partícula começa na origem em , então .
Observe que cada quadrado da grade na Figura P2.27 tem “área”:
.
Podemos encontrar a área sob a curva e, assim, determinar , contando quadrados. Você pode ver que x = 35 m em t = 4 s porque existem quadrados abaixo da curva. Além disso, em porque os representados pelo meio quadrado entre são cancelados pelos –5 m representados pela metade do quadrado entre .
Áreas abaixo do eixo são áreas negativas. A partícula passa por em e novamente em .
Passo 2

Resposta
- e novamente em
