Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 5.Problemas - Ex. 19

No sistema da figura, a bolinha de massa m   está amarrada por fios de massa desprezível ao eixo vertical AB e gira com velocidade ω em torno desse eixo. A distância AB vale l. Calcule as tensões nos fios superior e inferior. Para que valor de ω o fio inferior ficaria frouxo?

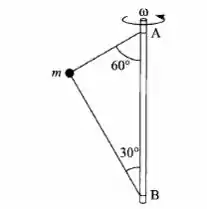
Passo 1

Primeiro vamos enxergar as forças atuantes na bolinha

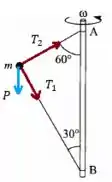
Para que a bolinha não caia as componentes verticais do sistema tem que equilibrar, vem comigo!

T 1 y + P = T 2 y

→

T 1 c o s 30 ° + m g = T 2 c o s 60 °

Já quando se trata das componentes horizontais existe uma resultante centrípeta de aceleração ω 2 r . Fica assim então

T 1 s e n 30 ° + T 2 s e n 60 ° = m ω 2 r

Pronto, já temos nosso sistema de equações!

T 1 c o s 30 ° + m g = T 2 c o s 60 ° T 1 s e n 30 ° + T 2 s e n 60 ° = m ω 2 r

Passo 2

Bora lá resolver essa, substituindo os valores que temos,

T 2 - T 1 3 = 2 m g   T 1 + T 2 3 = 2 m ω 2 r

Vamos multiplicar a segunda equação por 3 e somar as 2, show?

T 2 + 3 T 2 = 2 m     g + 3 ω 2 r

→

T 2 = m 2   g + 3 ω 2 r

Agora é só substituir na segunda equação pra achar T 1

T 1 = 2 m ω 2 r - m 2 3 g + 3 ω 2 r

= m ω 2 r 2 - m 2 3 g

= m 2 ω 2 r - 3 g

Galera, nós achamos nossas trações em função do raio de rotação, mas não temos esse dado no enunciado e sim a distância AB do cabo, bora achar o raio então, vem comgio!

Vamos escrever as áreas do triângulo de 2 maneiras diferentes, saca só

A t = x y 2

Também temos

x s e n 60 ° = r

y s e n 30 ° = r

→

A t = r 2 2 s e n 60 ° .   s e n 30 ° = 2 r 2 3

Além disso, nossa área também pode ser escrita assim

A t = l r 2

→

l r 2 = 2 r 2 3

→

r = l 3 4

Bora substituir de volta nas trações, finalmente temos

T 1 = m 2 ω 2 l 3 4 - 3 g

= m 2 3 ω 2 l 4 - g

T 2 = m 2   g + 3 ω 2 l 3 4

= m 2 3 ω 2 l 4 + g

Passo 3

Só falta agora achar a velocidade para a qual o fio de baixo ficaria frouxo. Galera, isso acontece quando a tração T 1 = 0  

m 2 3 ω 2 l 4 - g = 0

→

ω 2 l 4 - g = 0

→

ω 2 = 4 g l

→

ω = 2 g l

Sabemos que s e   ω <   2 g l então acorda de baixo afrouxaria.

Resposta

T 1 = m 2 3 ω 2 l 4 - g

T 2 = m 2 3 ω 2 l 4 + g

ω m í n = 2 g l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Tr��s trenós estão sendo puxados horizontalmente sobre uma superfície de gelo horizontal e sem atrito, através de cordas horizontais (Figura 5.50 ). A força de puxar é horizontal e possui módulo de 12
Peso aparente. Um estudante de física de 550N está sobre uma balança portátil apoiada sobre o piso de um elevador de 850k g (incluindo o estudante), que está suspenso por um cabo. Quando o elevador co
Uma corda leve está amarrada a um bloco com massa de 4,0k g , que está em repouso sobre uma superfície horizontal e sem atrito. A corda horizontal passa por uma polia sem atrito e sem massa, e um bloc
Duas caixas, uma de massa 4 k g e outra de 6 k g , estão em repouso sobre a superfície sem atrito de um lago congelado, ligadas por uma corda leve ( f i g u r a4.38 ) . Uma mulher usando um tênis de s
Uma rua de São Paulo possui uma inclinação de 17,5 ° com a horizontal. Qual é a força paralela à rua necessária para impedir que um carro de 1390k g desça a ladeira dessa rua?