Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Exercício - Ex. 6b
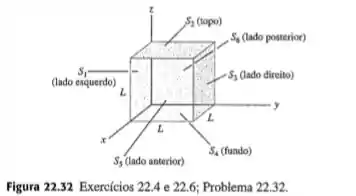
Um cubo possui uma aresta de comprimento . Ele é colocado com um cértice na origem, como indica a Figura . O campo elétrico não é uniforme, mas é dado por . Qual é o fluxo elétrico através de cada uma das seis faces do cubo , , e ? Determine o fluxo elétrico total no interior do cubo.
Passo 1
Visto que duas das faces do cubo não possuem fluxo elétrico a partir do campo elétrico, o fluxo total será dado pela soma do fluxo existente.
Passo 2
Dessa forma:
Isso mostra que o campo elétrico sai e também entra pelo cubo já que é uniforme.
Resposta
Exercícios de Livros Relacionados
O cubo da Fig. 23-27 tem 1,40 m de aresta e está orientado da forma mostrada na figura em uma região onde existe um campo elétrico uniforme. Determine o fluxo elétrico através da face direita do cubo,
Um campo elétrico dado por E = 4,0î – 3,0(y2 + 2,0)ĵ atravessa um cubo gaussiano com 2,0 m de aresta, posicionado da forma mostrada na Fig. 23-5. (E é dado em Newtons por coulomb e x em metro .) Deter
O fluxo de campo elétrico em cada face de um dado tem um valor absoluto, em unidades de 10 3 N · m 2 / C , igual ao número N de pontos da face ( 1 ⩽ N ⩽ 6 ). O fluxo é para dentro se N for ímpar e par
Uma esfera com 6,00 cm de raio possui uma densidade de cargas uniforme de 500 n C / m 3 . Considere uma superfície gaussiana cúbica concêntrica com a esfera. Determine o fluxo elétrico através da supe
A água em uma vala de irrigação de largura w = 3,22 m e profundidade d = 1,04 m corre com uma velocidade de 0,207 m / s . O fluxo de mássico da água através de uma superfície imaginária é o produto da