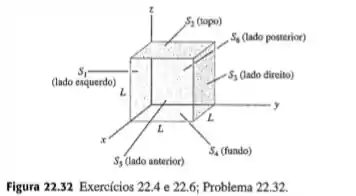
Um cubo possui arestas com comprimento e é colocado com um dos vértices na origem, como indica a Figura . O campo elétrico não é uniforme, porém é dado por , onde e são constantes positivas. Determine o fluxo elétrico através de cada uma das seis faces do cubo , , e . Calcule o fluxo elétrico total no interior do cubo.
Passo 1
Eq. (22.3) para calcular o fluxo. Identifique a direção do vetor unitário normal para cada
superfície.
- Adicione o fluxo através de cada uma das seis faces:
Agora, podemos encontrar o valor do fluxo em cada lado do cubo. Então, devemos calcular de acordo com os vetores que tem os vetores para o mesmom sentido:
Face
Face
Face
Face
Face
Face
Passo 3
O fluxo elétrico total por todos os lados é zero
Resposta
Vide a explicação