Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 96
Considere uma estrada molhada com inclinação lateral como no Exemplo (Seção ), no qual há um coeficiente de atrito estático de e um coeficiente de atrito cinético de entre os pneus e a estrada. O raio da curva é .
- Se o ângulo de inclinação lateral for qual é a velocidade máxima que um carro pode ter antes que ele deslize para cima do plano inclinado?
- Qual a velocidade mínima que um carro pode ter antes que ele deslize para baixo do plano inclinado?
Passo 1
Fala galera! Tudo bem? Essa questão parece difícil, mas vamos com calma!
Aqui temos um carro em uma curva inclinada, onde a normal (representada em laranja) está inclinada de e temos também a força de atrito (que aponta na direção radial, pois essa seria a trajetória do carro, e está em azul). Não esqueça que o peso (em verde) sempre está presente e aponta para baixo.
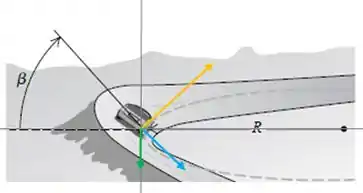
O ângulo é o ângulo que a normal faz com o eixo vertical, bem como a força de atrito, mas para baixo do eixo horizontal positivo. Dessa forma teremos essas duas forças com componentes horizontais e verticais. Vou colocar as componentes de forma tracejada para você visualizar melhor, saca só:
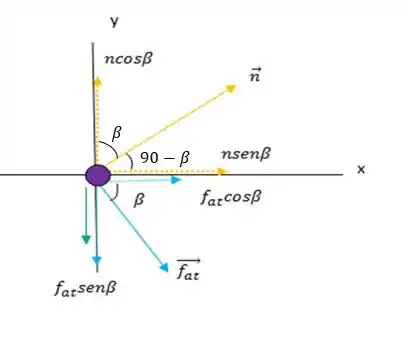
Assim na vertical vamos ter três forças: para cima a componente vertical da normal e para baixo a força peso e a componente vertical da força de atrito. Essas forças estão em equilíbrio, pois não há movimento do carro na vertical.
Na horizontal temos duas forças, e elas apontam para o mesmo lado: as componentes horizontais da força normal e da força de atrito. Elas compõem o movimento do carro e são iguais à força centrípeta, pois o carro está em movimento circular nesse momento, tranquilo?
Tranquilo até aqui? Agora vou colocar isso tudo em um sistema de coordenadas e vamos equacionar essas forças, ok?
Para as duas situações, vamos poder utilizar o mesmo sistema de coordenadas, só vamos prestar um pouco de atenção nos sinais, mas isso eu volto a lembrar você mais tarde =)
Passo 2
- Antes de achar a velocidade, precisamos achar a aceleração! Vamos usar essa fórmula aqui:
- Agora o diagrama de corpo livre dessa situação é igual ao da letra , com a exceção que as componentes de têm direções opostas! E aqui que temos que ter atenção nos sinais! As equações de força ficam as mesmas, a não ser pela mudança no sinal dos termos que contém . Assim, resgatando a expressão para a aceleração lá do passo anterior e fazendo a mudança de sinais teremos o seguinte:
A aceleração é radial (por se tratar de um movimento curvilíneo) e aponta para o centro da trajetória que, nesse caso, aponta para a direita. Para achar a aceleração vamos precisar separar as componentes!
A força normal tem componentes, vertical e horizontal:
A força de atrito também tem duas componentes, vertical e horizontal:
A última força a ser considerada é o peso,
Fazendo os balanços das forças. Na direção vertical:
Lembrando que , temos:
Na horizontal:
E juntando as duas relações teremos:
Agora vamos substituir os valores!
Passo 3
Como o ângulo foi dado e o coeficiente de atrito é , ficou tranquilo determinar a aceleração:
E agora podemos voltar lá para o passo anterior e resgatar a relação da aceleração e da velocidade:
A aceleração é e o raio foi dado no enunciado e vale , agora é só substituir:
Passo 4
E a velocidade mínima:
Prontinho!