Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 97

Para que você possa percorrer a estrada com uma rapidez , mesmo quando está congelada (), qual deve ser a inclinação? Vamos fazer um diagrama:

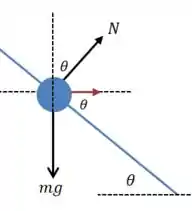
A seta vermelha indica a direção da resultante centrípeta, ficamos apenas com uma componente da normal nessa direção:

E na direção vertical, para que haja equilíbrio, teremos:

Essas duas equações formam um sistema que podemos resolver para encontrar . Pela segunda equação temos que:

Substituindo isso na segunda:

Beleza, agora sabemos a inclinação da estrada. Agora considerando vamos encontrar a rapidez mínima em que não há derrapagem.

Quando estamos próximos da rapidez mínima, a tendência é que o carro derrape para dentro da curva, então o diagrama fica da seguinte forma:

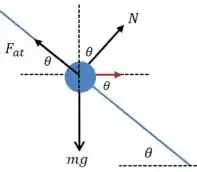
Vamos montar as equações em cada uma das direções. Na horizontal precisamos de uma resultante centrípeta:

E na vertical precisamos do equilíbrio:

Quando a rapidez é mínima, estamos exigindo o máximo da força de atrito, então podemos usar a seguinte relação:

Substituindo isso nas duas equações de cima, ficamos com um sistema:

Nosso objetivo é encontrar , então vamos dividir a primeira equação pela segunda:

E agora é só substituir e :

E para encontrar o caso máximo, vamos fazer praticamente a mesma coisa, mas dessa vez o atrito será forçado no sentido oposto:

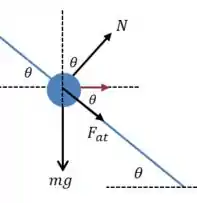
Ao invés de refazer a conta inteira, vamos simplesmente trocar o sinal dos termos com na equação final, e trocar por :

E então o intervalo permitido para a rapidez é:

O intervalo entregue à polícia seria .