Um bloco de de massa repousa na superfície inclinada de uma cunha de de massa, como na figura. Uma força horizontal é aplicada sobre a cunha, que desliza sobre uma superfície sem atrito. (a) Se o coeficiente de atrito estático entre a cunha e o bloco é e a cunha tem uma inclinação de com a horizontal, encontre os valores máximo e mínimo da força para os quais o bloco não escorrega. (b) Repita a parte (a) com .
Passo 1
Dessa vez temos uma força aplicada na direção paralela ao chão, então vamos usar um sistema de coordenadas que seja útil para tratar desse caso:
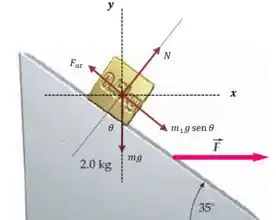
(Aproveitamos o diagrama do enunciado por conveniência, mas o ideal seria desenhar o bloco como um ponto). Vamos escrever as equações das forças, começando pela horizontal:
E então a vertical:
Passo 2
O que colocamos na equação da força horizontal é a aceleração do sistema inteiro (bloco e cunha), ou seja:
E queremos achar os valores máximo e mínimo dessa força para que o bloco não deslize.
Quando a força é mínima, a preocupação é que o bloco não deslize para baixo, então temos que garantir que o átrio é forte o suficiente para segurá-lo onde está:
Substituindo isso na equação das forças verticais:
Substituindo isso tudo na equação das forças horizontais:
Dividindo tudo por e isolando a aceleração :
E esse é o valor mínimo da aceleração, e a força mínima associada é:
Passo 3
E para encontrar o valor máximo é só inverter a lógica. Agora nossa preocupação é que o bloco deslize para cima, então queremos garantir que a força de atrito estático (agora apontando para baixo) é suficiente para segurá-lo onde está:
Nem precisamos refazer a conta toda, é só inverter o sinal dos termos em que o aparece (que afinal de contas são os termos ligados à força de atrito):
E essa é a aceleração máxima, associada à seguinte força:
Passo 4
(b) Agora só precisamos refazer essas contas para o caso em que . Já temos as fórmulas prontas, só falta trocar os valores.
Para a força mínima temos:
E para a força máxima:
Resposta
(a) e , com .
(b) e , com .